Exothermic reactions cause their immediate surroundings to become warmer, because they are releasing heat into their surroundings. Think of a campfire, for example. When you sit next to the fire, you feel warmth. This is the heat being released by the exothermic reactions in the flames.
Endothermic reactions cause their immediate surroundings to become cooler, because they are absorbing heat from (that is, taking heat away from) their surroundings. If you put an ice cube in your hand, it will melt faster, because your warm hand can supply heat for the endothermic melting process. At the same time, you hand feels cold, because it is losing heat to the endothermic process.
Heat is a form of energy. It is energy in transit. Heat is the form of energy that flows between two objects that are in thermal contact but are at different temperatures. We normally measure heat energy in units of joules (abbreviation: J) or kilojoules (abbreviation: kJ) where
1 kJ = 1000 J
We usually recognize the flow of heat by an associated temperature change. When heat flows into an object, its temperature increases and when heat flows out of an object, its temperature decreases.
We use the algebraic symbol q to represent heat flow. The sign convention is that when heat flows into an object, that object has a positive q, and when heat flows out of an object, that object has a negative q.
We represent temperature changes by the algebraic symbol Dt where
Dt = tf - ti
with tf representing the final temperature and ti representing the initial temperature.
Example 1
If a block of aluminum metal starts out at a temperature of 18.3 oC and is warmed to 75.9 oC, what is the tempeature change for the block of metal?
Solution
The block of aluminum starts out at 18.3 oC, so this is its initial temperature, that is,
ti = 18.3 oC
The block of aluminum ends up at 75.9 oC, so this is its final temperature, that is,
tf = 75.9 oC
The temperature change can then be calculated:
Dt = tf - ti = 75.9 oC - 18.3 oC = 57.6 oC
Notice we get a positive answer. The sign convention is that warming is represented by a positive Dt and cooling is represented by a negative Dt.
Example 2
A cup of coffee at 85.6 oC cools to a temperature of 24.8 oC. What is the temperature change for the cup of coffee?
Solution
The cup of coffee starts out at 85.6 oC, so that is its initial temperature. That is,
ti = 85.6 oC
The cup of coffee ends up at 24.8 oC, so that is its final temperatrue. That is,
tf = 24.8 oC
We can now calculate the temperature change:
Dt = tf - ti = 24.8 oC - 85.6 oC = -60.8 oC
Note that the answer is negative in this case. That sign convention is that negative values of Dt represent cooling.
The equation relating the heat flow with respect to an object to its resulting temperature change is
q = s . m . Dt
where q is the heat, s is a constant called the specific heat, m is the mass, and Dt is the temperature change. The specific heat varies from one substance to the next and must be looked up in a table. You can find a table listing a few specific heats on page 246 of your Hill & Petrucci textbook (Table 6.1).
Example 3
How much heat is required to raise the temperature of 675.10 g of aluminum from 5.8 oC to 97.4 oC?
Solution
The equation relating heat flow and temperature change is
q = s . m . Dt
Looking up the specific heat for aluminum in Table 6.1 on page 246 of the textbook, we find that
s = 0.902 J / g oC
The mass was given to be 675.10 g, which we assign to the variable m:
m = 675.10 g
In this problem, the initial temperature is 5.8 oC and the final temperature is 97.4 oC. From these temperatures, we can calculate the temperature change:
Dt = tf - ti = 97.4 oC - 5.8 oC = 91.6 oC
Now we have all the required values, so we can calculate the heat:
q = s . m . Dt = ( 0.902 J / g oC ) . ( 675.10 g ) . ( 91.6 oC) = 55779 J
When we deal with such large numbers of joules, we normally convert them to kilojoules:
55779 J x 1 kJ
= 55.779 kJ =
approx. 55.8 kJ
1000 J
I have rounded the final answer to 3 significant figures to reflect the accuracy of the data that lead to it.
Example 4
How much heat must be lost by 783.21 g of copper to lower its temperature from 68.7 oC to 22.1 oC?
Solution
Looking up copper in Table 6.1 on page 246 of Hill & Petrucci, we find that
s = 0.385 J / g oC
The mass is given to us in the problem, and we make the assignment
m = 783.21 g
The initial temperature is 68.7 oC and the final temperature is 22.1 oC, and from these, we can calculate the temperature change:
Dt = tf - ti = 22.1 oC - 68.7 oC = -46.6 oC
Now that we have all the values, we can calculate the heat:
q = s . m . Dt = ( 0.385 J / g oC ) . ( 783.21 g ) . ( -46.6 oC) = -14052 J
Converting to kJ:
-14052 J x 1
kJ =
-14.052 kJ = approx. -14.1
kJ
1000 J
Thus, the amount of heat that must be lost is 14.1 kJ. The negative sign indicates that this is a heat loss.
A slightly more complicated problem is one in which the starting temperature and the amount of heat is given and you must find the final temperature.
Example 5
A 594.21 g sample of water at 22.3 oC absorbs 55.16 kJ of heat. What is the temperature of the water after absorbing this heat?
Solution
We must first calculate how much the temperature will change, then we can use the temperature change and the initial temperature to find the final temperature. We take the equation
q = s . m . Dt
and divide both sides by s . m to solve for Dt. This gives us
Dt =
q
s . m
We must be careful about consistency of units in working this problem. Since s has energy expressed in units of J, we can't express q in units of kJ. The same units must be used for energy throughout the problem. This is true of any physical quantity in any calculation. We must convert the energy we have been given from kJ to J:
55.16 kJ x 1000 J
= 55160 J
1 kJ
Looking up the specific heat of water in Table 6.1 on page 246 of Hill & Petrucci, we find that
s = 4.182 J / g oC
Reading the problem, we see that
m = 594.21 g
And from our earlier conversion:
q = 55160 J
We can now calculate the temperature change:
Dt =
q =
55160 J
= 22.20 oC
s . m
( 4.182 J / g oC ) . ( 594.21 g )
Then, from the equation
Dt = tf - ti
we can solve for tf to get
tf = Dt + ti = 22.20 oC + 22.3 oC = 44.50 oC = approx. 44.5 oC
The final answer has been rounded to one decimal place in accordance with significant figure rules for addition.
Example 6
A 744.90 g sample of water at 93.4 oC loses 51.83 kJ of heat. What is the temperature of the water after losing this heat?
Solution
This problem is worked like the previous one except that it is a heat loss rather than a heat gain. This means we must enter the heat (q) as a negative number. That's really the only difference. As before, we solve the equation
q = s . m . Dt
to get
Dt =
q
s . m
Again, we must convert the heat to J for consistency of units:
-51.83 kJ x 1000
J = -51830 J
1 kJ
Therefore,
q = -51830 J
The other variables we need are
s = 4.182 J / g oC
and
m = 744.90 g
Now we can calculate the temperature change:
Dt =
q =
-51830 J
= -16.64 oC
s . m
( 4.182 J / g oC ) . ( 744.90 g )
Notice that we get a negative Dt. This is to be expected where cooling is taking place. Now as before, we solve the equation
Dt = tf - ti
for Dt to get
tf = Dt + ti = ( -16.64 oC ) + 93.4 oC = 76.76 oC = approx. 76.8 oC
It is important to remember that Dt is negative when solving for tf. The final answer has been rounded off to one decimal place in accordance with significant figure rules for addition.
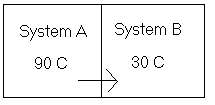
So far, we have worked with one system at a time, but the most interesting considerations are those in which two or more subsystems are in thermal contact to make up a "macrosystem". For simplicity, we will consider the macrosystem to be isolated from the surroundings, so that we don't have the complicating feature of heat loss to or gain from the surroundings. In this simplified case, the only heat flows possible are simply exchanges of heat among the subsystems of the macrosystem. Lets begin this consideration in the simplest way possible, with a macrosystem having only two components.

Here, System A and System B are in thermal contact but isolated from the surroundings (the isolating insulation is not shown in the diagram). System A is at 90 oC but System B is only at 30 oC, so heat will spontaneously flow from System A to System B, as shown by the arrow drawn in the diagram. As System A loses heat, its temperature will drop. At the same time, System B is gaining heat, so its temperature will rise. Eventually, a time will come when the two systems are at the same temperature. We call this thermal equilibrium. After thermal equilibrium has been reached, no net heat flow occurs between the two systems.
Suppose that at the moment that thermal equilibrium was reached, a total of 10 kJ of heat had left System A. This would mean that
qA = -10 kJ
Recall that the q has to be negative when the heat leaves the system. But where did that heat that left System A go? It entered System B, of course, since we said the 2-compartment system was isolated from the surroundings. All the heat that leaves System A must enter System B -- there is nowhere else for it to go. Therefore, 10 kJ of heat enters System B.
qB = +10 kJ
In other words, one q value is equal to the negative of the other:
qA = -qB or -qA = qB
We can re-write the above relationship in the form
qA + qB = 0
This may seem like just a trivial algebraic re-arrangement of what we already have, but it is desirable to write it in this way because it better illustrates the Law of Conservation of Energy. This law tells us that energy can be neither created nor destroyed. Because of this, the sum of all the heat fluxes in an isolated multi-component system must be zero. Written in this form, we can easily extend the expression to include systems containing more than 2 components. For example, consider a 5-component system.

The law of conservation of energy dictates that
qA + qB + qC + qD + qE = 0
If you know the total overall heat flux for all the components but one, you can calculate the one unknown heat flux.
Example 7
Consider 5 systems that are in thermal contact and initially are all at different temperatures. After a re-distribution of heat among these systems, thermal equilibrium is reached (i.e., they are all at the same temperature). The following is a description of the heat flow with respect to four of these systems:
System A lost 12 kJ of heat
System B gained 6 kJ of heat
System C lost 10 kJ of heat
System D gained 5 kJ of heat
What happened to System E?
Solution
Remembering that heat gain is positive and heat loss is negative, we can make the following variable assignments from the above heat flow descriptions:
qA = -12 kJ
qB = +6 kJ
qC = -10 kJ
qD = +5 kJ
Applying the Law of Conservation of Energy to this problem, we have
qA + qB + qC + qD + qE = 0
and solving this for qE gives
qE = -( qA + qB + qC + qD)
and substituting values we have
qE = -( -12 kJ + 6 kJ + { -10 kJ } + 5 kJ )
qE = -( -11 kJ ) = +11 kJ
Since we get a positive value for qE, we know System E gains heat. Therefore, our final answer to this problem is that System E gains 11 kJ of heat.
A practical application of the concept of a multi-component system is determining the specific heat of a metal. This is one of the experiments we do at Palo Alto in CHEM 1111 (General Chemistry Laboratory) and it works as follows.
We first heat a metal sample of known mass by putting it in a test tube and submerging it in boiling water. After a few minutes in the boiling water, the metal will reach the same temperature as that of the water (thermal equilibrium).
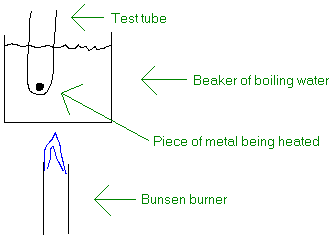
Then, in a styrofoam coffee cup, we have a known mass of water at room temperature (typically 25 oC). Then the hot metal is quickly transferred from the test tube to the water in the coffee cup. Since the metal typically starts out at a temperature of around 100 oC, while the water in the coffee cup is around 25 oC, there will be a transfer of heat from the metal to the water. This flow of heat will continue until the metal and the water reach the same temperature. By recording the maximum temperature of the water in the coffee cup, we have the final temperature of both the metal and the water. Since the two initial temperatures are known, we can find both Dtmetal and Dtwater. From these, we can calculate smetal.
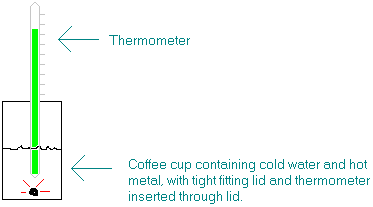
In the above apparatus, we will assume for simplicity that all the heat lost by the metal is gained by the water. We will ignore any heat absorption by the styrofoam and any loss of heat to the surroundings. In such a two-component system, we have seen that one of the q values is the negative of the other -- a special case of the Law of Conservation of Energy. For the above apparatus, we can write
qmetal = -qwater
We can expand both q's using the general relation
q = s . m . Dt
but we must label all the variables as referring to metal or water, as appropriate.
smetal . mmetal . Dtmetal = -swater . mwater . Dtwater
Solving this equation for smetal gives
-swater . mwater . Dtwater
smetal = ______________________
mmetal . Dtmetal
Everything on the right side of the above equation can be readily determined in a laboratory experiment like that depicted in the previous two drawings, giving us a simple technique for measuring specific heats.
Example 8
A 5.186 g sample of an unknown metal was heated to 100.0 oC by placing it in a test tube submerged in boiling water. The metal was then dropped into 25.000 g of water at 24.8 oC in a coffee cup calorimeter. The water in the calorimeter warmed up to 28.5 oC. What is the specific heat of the metal? Note that the specific heat of water is 4.182 J / g oC.
Solution
We can calculate smetal using the equation derived earlier:
-swater . mwater . Dtwater
smetal = ______________________
mmetal . Dtmetal
We must calculate the Dt values; the other variables are given in the problem.
Dtwater = 28.5 oC - 24.8 oC = 3.7 oC
Dtmetal = 28.5 oC - 100.0 oC = -71.5 oC
swater = 4.182 J / g oC (given)
mwater = 25.000 g (given)
mmetal = 5.186 g (given)
Now use the values in the formula
( -4.182 J / g oC ) . ( 25.000 g ) . (
3.7 oC )
smetal =
_________________________________________
( 5.186 g ) . ( -71.5 oC)
smetal = 1.0 J / g oC
Not only can we release heat into a calorimeter by dropping hot metal into it, as in the previous example, we can also release heat into a calorimeter by running an exothermic reaction in it. Or, we can run an endothermic reaction in a calorimeter and watch its temperature fall. By measuring the temperature change inside a calorimeter associated with a chemical reaction, we can determine the heat flux of that chemical reaction. The following example, which is taken from Examples 6.11 and 6.12 on pages 250-251 in your Hill and Petrucci textbook, shows how this is done.
Example 9
The reaction
HCl(aq) + NaOH(aq) ----------> H2O(l) + NaCl(aq)
is exothermic. To measure the heat of this reaction a 50.0 mL volume of 0.250 M HCl was mixed with a 50.0 mL volume of 0.250 M NaOH in a coffee cup calorimeter. Both solutions had a temperature of 19.50 oC before mixing, but after mixing, the temperature increased to 21.21 oC. Calculate the amount of heat released in the chemical reaction, and the amount that would be released for the reaction of 1 mole of HCl and NaOH, as indicated by the balanced equation.
Solution
The chemical reaction is a process, not a physical substance, but nevertheless, we can talk about a qrxn and write out an equation like that for two systems in thermal contact.
qrxn = -qcal
The qrxn can not be expanded in terms of s, m and Dt but qcal can be. For simplicity, we consider the calorimeter to consist of its contents only -- that is, we ignore the styrofoam from which the cup is constructed, and as before, in our calculations, we will ignore any absorption of heat by the styrofoam or loss of heat to the surroundings.
qrxn = -scal . mcal . Dtcal
We will need to make some further assumptions to obtain the values of
the variables on the right side of this equation.
We can now calculate q for the chemical reaction.
Dtcal = 21.21 oC - 19.50 oC = 1.71 oC
qrxn = ( -4.182 J / g oC ) . ( 100 g ) . ( 1.71 oC ) = -715 J
Thus the reaction -- using the actual amounts of HCl and NaOH that we had available -- releases 715 J of heat. However, we usually express the amount that would be released (or absorbed in the case of endothermic reactions) for the reaction as written, putting the molar interpretation on the coefficeints. Recall that the balanced chemical equation for the reaction we are dealing with here is
HCl(aq) + NaOH(aq) ----------> H2O(l) + NaCl(aq)
which refers to 1 mole of HCl and 1 mole of NaOH. But these are not the amounts of these substances we actually used. How much of each did we really have?
For both solutions, the volume was 50.0 mL and the concentration was 0.250 M. The abbreviation M stands for mol / L. Thus, if we had 1 liter of the HCl solution, we would have 0.250 moles of HCl. Likewise, if we had 1 liter of the NaOH solution, we would have 0.250 moles of NaOH. But we don't have 1 liter of these solutions, we have 50.0 mL -- considerably less than 1 liter, so we will have considerably less than 0.250 moles of each reactant. We can calculate the number of moles as shown below.
50.0 mL x 1 L
x 0.250 mol =
0.0125 mol
1000 mL
1 L
Only one calculation was needed because both solutions had the same volume and the same concentration; if that had not been the case, we would have needed a separate calculation for each solution.
Now we know that the 715 J was released for 0.0125 moles of each reactant, so we can calculate what it would have been if we had used 1 mole of each reactant.
-715 J
x 1 mol =
-57200 J
0.0125 mol
Large numbers of joules like the above are usually re-expressed in kJ
-57200 J x 1000 J
= -57.2 kJ
1 kJ
From the above example, it would seem that we now have the tool to measure the heat of any reaction -- the calorimeter. But as we will see shortly, there are some reactions that just don't lend themselves to being measured in this way. However, we will learn of a powerful principle called Hess' law, that will sometimes allow us to calculate the heats of some reactions that we can not directly measure. Before we do this, however, we need to learn some additional terminology. From the previous problem, we can write the following thermochemical equation:
HCl(aq) + NaOH(aq) ----------> H2O(l) + NaCl(aq) qrxn = -57.2 kJ
But you will often see it written in this way:
HCl(aq) + NaOH(aq) ----------> H2O(l) + NaCl(aq) DH = -57.2 kJ
You have encountered the symbol D before, and as you probably remember, it refers to a change in something. But what is this H that comes after the D and what are we changing when we change H? H is a thermodynamic function called enthalpy. At an introductory level, we can think of enthalpy as "stored up heat". Each chemical substance has a certain amount of chemical potential energy. When a chemical reaction converts substances of high potential energy to substances of low potential energy, the difference in energy appears as heat -- that is, we have an exothermic reaction. Conversely, if a chemical reaction converts substances of low potential energy into substances of high potential energy, the reaction must absorb energy in order to occur -- it will be an endothermic reaction.
If we knew the absolute chemical potential energy (enthalpy) of each substance, we could calculate the heat of reaction (enthalpy) without ever having to measure it. Our calculation would proceed as follows:
Initially, our system consists of HCl(aq) and NaOH(aq). Denoting HHCl(aq) as the enthalpy of one mole of HCl(aq) and HNaOH(aq) as the enthalpy of one mole of NaOH(aq), our initial enthalpy would be given by
Hi = HHCl(aq) + HNaOH(aq)
After the reaction is over, we have H2O(l) and NaCl(aq) in place of the original HCl(aq) and NaOH(aq). Denoting HH2O(l) as the enthalpy of one mole of H2O(l) and HNaCl(aq) as the enthalpy of one mole of NaCl(aq), we have, for the final enthalpy,
Hf = HH2O(l) + HNaCl(aq)
The change in enthalpy would then be given by
DH = Hf - Hi = ( HH2O(l) + HNaCl(aq) ) - ( HHCl(aq) + HNaOH(aq) )
In this reaction, the enthalpy of the reactants (HCl and NaOH) is larger than the enthalpy of the products (H2O and NaCl) so heat is released as the reaction occurs -- that reaction is exothermic. The amount of energy released as heat is equal to the difference in chemical potential between the reactants and products.
The equation presented above for calculating DH is only useful for theoretical discussions; it has no practical value. This is because the individual enthalpies depicted in the equqation are impossible to measure. We can not determine the absolute amount of energy locked up in a chemical system. We can only measure changes in energy as reactions proceed. We will get around this problem by picking an arbitrary reference point to set as the zero of energy, and expressing the enthalpies of chemical substances against that reference. This is something like using sea level as the zero reference for measuring altitude. To develop this concept, let's use a reaction that is simpler than the acid base neutralization reaction. Let's pick one that has only chemical elements as reactants, and forms a single product.
C(gr) + O2(g) ----------> CO2(g) DH = -393.5 kJ
Recall that DH is the same thing as qrxn (provided the reaction is run at constant pressure -- which is usually the case). Thus the value quoted above can be measured in the laboratory. Now let us revisit that theoretical formula one more time, to see how we can solve the problem of not being able to measure absolute enthalpies.
DH = Hf - Hi = HCO2(g) - ( HC(gr) + HO2(g) )
We don't know the absolute enthalpies of graphite, oxygen, and carbon dioxide, so we can not directly calculate DH for the reaction. But we can measure it experimentally, so we know the answer -- if we could calculate it -- would be -393.5 kJ. We can picture the following "energy hill" for the reaction:
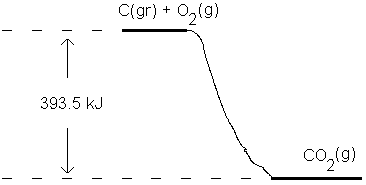
The procedure chemists have adopted is to arbitrarly set the elements in their most stable states to have zero enthalpy. On this basis, the top of the hill shown above has a zero value for the enthalpy, since only elements appear there. Since the hill is 393.5 kJ high, and CO2 is at the bottom of the hill, its enthalpy -- on a relative scale -- must be -393.5 kJ. That is, a mole of CO2 is 393.5 kJ lower in energy than a that of a mixture containing a mole of graphite and a mole of oxygen.
This is the way the enthalpies of ALL compounds are tabulated -- as a relative value compared to the elements which compose the compound. We can look these values up in tables. Only the compound will be listed, but we must remember that the value listed is for the chemical reaction forming one mole of the compound directly from the elements in their most stable states. The value listed is NOT a value pertaining solely to the compound itself, because there is no way to determine absolute enthalpies.
As a test of your understanding of the thermochemical table, look up the DHf value for liquid water. In your Hill & Petrucci textbook, it is on page A16. You will find that the value is -285.8 kJ. Note that the state in which the substance exists is significant when you are doing thermochemistry. The DHf for gaseous water has a different value (-241.8 kJ). Now, can you write the balanced chemical equation for which the DH value is -285.8 kJ?
Recall that the values listed in the table are the DH
values for the reactions in which one mole of the compound is formed directly
from the elements in their most stable states. Water is composed
of the elements hydrogen and oxygen, and for both of these elements, the
most stable state at standard temperature (
H2(g) + O2(g) ----------> H2O(l)
In the past, we probably would have balanced this by putting a coefficient of 2 in front of H2 and H2O to get
2H2(g) + O2(g) ----------> 2H2O(l)
but in our work on thermochemistry, we want to form one mole of the compound (not two) because that's the way the values in the table are given. Therefore, we will need to divide this equation by 2 to show only one mole of water being formed.
H2(g) + ½O2(g) ----------> H2O(l) DH = -285.8 kJ
The above reaction is the one being referred to in Appendix C.1, when it associates the substance H2O with the DH value -285.8 kJ. Notice that the table refers to the values it provides as DHf values. The subscript f stands for "formation". A formation reaction is one in which a compound is formed directly from the elements in their stable states. The left hand side of a formation reaction will always contain free elements, so it is sufficient to list the formula of the compound they form when reporting the DH values in a table. The left hand side of the equation is obvious from looking at the elements that make up the compound. Furthermore, thermochemical tables always list molar enthalpies of formation. That is, the enthalpy change when the elements in their stable states form one mole of the compound. I used these facts to figure out the formation reaction for liquid water, as explained above.
In working with thermochemical equations, it will often be necessary
to manipulate them in a mathemical sense. The most common ways thermochemical
equations are altered are reversing their direction and multiplying (or
dividing) them by a constant. We need to know how to adjust the value
of DH when we change the way we choose to write
an equation. The following are two very important concepts for thermochemical
work:
C(gr) + O2(g) ----------> CO2(g) DH = -393.5 kJ
Written in this direction, the DH is -393.5 kJ, because we must start at the top of the hill and go down, decreasing in energy as we go. Since the hill is 393.5 kJ high, we lose 393.5 kJ of energy in going from the top to the bottom, thus explaining the DH of -393.5 kJ. But now suppose we write the reaction in the opposite direction, that is
CO2(g) ----------> C(gr) + O2(g) DH = +393.5 kJ
To carry out this reaction, we would have to start at the bottom of the hill instead of the top. This time, our journey would take us up the hill, not down. We would be increasing in energy as we go. Since the hill is 393.5 kJ high, our energy would increase by 393.5 kJ in going from the bottom to the top. This the DH this time would be +393.5 kJ. The hill is still the same size, but we are going in the opposite direction.
The second concept is also fairly easy to understand. If a reaction is exothermic, for example, I can get more heat from it if I use a larger quantity of reactants. Think of a fire in a fire place. You can get more heat by burning a large pile of big logs than a small collection of twigs.
Earlier in these notes, I showed (using the HCl + NaOH reaction) how the DH of a reaction can be measured in a calorimeter. However, not every reaction can be measured in this way. Sometimes, a particular reaction may be impossible to carry out in the lab, or it may suffer interference from competing side reactions that render the measurements inaccurate. Forturnaely, it is sometimes possible to obtain the DH values for reactions we can not measure from those that we can measure. The following example illustrates this.
Let's say you would like to measure the DH for the following reaction, which we shall refer to as the "target reaction", since it is the one under study:
(target reaction) 2C(gr) + O2(g) ----------> 2CO(g) DH = ?
This reaction is exothermic, so you would like to measure its heat release in a calorimeter and calculate the DH in the same way as was done in the acid / base neutralization reaction done earlier. There is a problem, however. When you attempt to run this reaction, two other reactions also occur:
(reaction 1) C(gr) + O2(g) ----------> CO2(g) DH = -393.5 kJ
(reaction 2) 2CO(g) + O2(g) ----------> 2CO2(g) DH = -566.0 kJ
Since these two side reactions are also exothermic (note that exothermic reactions have negative DH values), the heat release you measure in the calorimeter will be a combination of the heat release from all three reactions. This makes your measurement inconclusive. You don't know how much of the heat you measured actually came from the target reaction, and you don't know how much of the graphite got used in the target reaction, as opposed to being used in reaction 1.
It turns out however, that the two side reactions, called "reaction 1" and "reaction 2" in these notes, can be measured in the absence of any competing reactions. What we want to do now is use the known (i.e. measured) values of DH for "reaction 1" and "reaction 2" to calculate the DH for the target reaction, which can not be directly measured.
The calculation we are about to embark on here is an application of Hess' Law, which tells us that if a reaction can be expressed as the sum of two or more other reactions, its DH value will be the sum of the DH values of those other reactions. Hess's Law works because enthalpy (H) and its change (DH) are state functions. A state function is one which is path independent.
Our target reaction converts 2 moles of graphite and 1 mole of oxygen into 2 moles of carbon monoxide. The change in enthalpy for this process depends only on the enthalpies of the graphite, the oxygen, and the carbon monoxide. It does not depend on how we carry out the change. The target reaction shows a direct conversion of graphite and oxygen into carbon monoxide, but as noted earlier, the direct conversion is not readily measurable. However, if we can design a multistep process (that is, consisting of 2 or more reactions) for which the net effect is the conversion of 2 moles of graphite and 1 mole of oxygen into 2 moles of carbon monoxide (i.e., the target reaction), the DH for the multistep process will be the same as that for the single step process. This must be true because as noted earlier, DH is a state function. Only the initial and final states are important, not the path taken to get from one to the other.
With all this as background, lets recall the 3 equations under consideration, and analyze how we can get the target reaction from reaction 1 and reaction 2.
(target reaction) 2C(gr) + O2(g) ----------> 2CO(g) DH = ?
(reaction 1) C(gr) + O2(g) ----------> CO2(g) DH = -393.5 kJ
(reaction 2) 2CO(g) + O2(g) ----------> 2CO2(g) DH = -566.0 kJ
It's really not that difficult to compare the known reactions to the target reaction and see how they must be adjusted to get the target. Follow allong with me and I'll explain my thought process as I go.
Looking at the target reaction, the first substance I see is graphite. I note that there are 2 moles of graphite on the left hand side of the equation. Then I look at the known reactions to see which one contains graphite. I see that reaction 1 contains graphite. Reaction 1 has the graphite on the left hand side, which I am happy with, since graphite appears on the left hand side of the target reaction. However, reaction 1 only provides 1 mole of graphite. This I am not happy with, because the target reaction has 2 moles of graphite. To solve this problem, I will multiply reaction 1 by 2, so it will have 2 moles of graphite, just like the target reaction. Note that I must multiply the entire reaction by 2, not just the graphite. If I only multiplied the graphite by 2, the equation would no longer be balanced. As explained earlier, when I multiply a reaction by a constant, I must multiply DH by that same constant. In this case, I am multiplying the reaction by 2, so I will need to multiply DH by 2. My set of equations now looks like this:
(target reaction) 2C(gr) + O2(g) ----------> 2CO(g) DH = ?
2 x (reaction 1) 2C(gr) + 2O2(g) ----------> 2CO2(g) DH = -787.0 kJ
(reaction 2) 2CO(g) + O2(g) ----------> 2CO2(g) DH = -566.0 kJ
Looking at the target reaction again, the second substance I see is oxygen. Since oxygen appears in both reaction 1 and reaction 2, it is not as easy to figure out what adjustments to make for it. This is one of few cases where it pays to procrastinate. Just skip oxygen for now, acknowledging that you will come back and take care of it later if absolutely necessary. Usually, it will not be necessary to return to a substance you skipped in this manner because the remaining substances will provide the information you need to make the other required adjustments.
Looking at the target reaction again, I note that the third substance
I see is carbon monoxide. I note that there are 2 moles of it, and
it is on the right hand side of the equation. Looking at the known
reactions, I see that carbon monoxide appears in reaction 2. I am
happy with the amount it provides (2 moles) but I am not happy with the
side of the equation it is on. It appears on the left hand side of
reaction 2, but it is on the right hand side in the target reaction.
This suggests that I should reverse the direction of reaction 2.
This will require that I change the sign of DH.
My set of equations now looks like this:
(target reaction) 2C(gr) + O2(g) ----------> 2CO(g) DH = ?
2 x (reaction 1) 2C(gr) + 2O2(g) ----------> 2CO2(g) DH = -787.0 kJ
(reverse reaction 2) 2CO2(g) ----------> 2CO(g) + O2(g) DH = +566.0 kJ
If you carefully examine the modified reactions, you will see that they now add up to the target reaction. When adding the reactions, we can cancel any substance that appears in equal amounts on both the left and right sides. This is somewhat reminiscent of canceling ions in ionic equations to get net ionic equations. Two moles of carbon dioxide, for example, appears on the right hand side of reaction 1 (as modified) but on the left hand side of reaction 2 (as modified). We can therefore cancel it out:
(target reaction) 2C(gr) + O2(g) ----------> 2CO(g) DH = ?
2 x (reaction 1) 2C(gr) + 2O2(g)
----------> 2CO2(g)
DH = -787.0 kJ
(reverse reaction 2) 2CO2(g)
----------> 2CO(g) + O2(g)
DH = +566.0 kJ
The oxygen is a bit more trickey, because even though it appears on both the left and right hand sides, it does not appear in equal amounts. In this case, there will be a partial cancelation: One of the 2 moles of O2 on the left hand side of reaction 1 (as modified) will cancel the 1 mole of O2 on the right hand side of reaction 2 (as modified). This will leave one mole of O2 on the left hand side of reaction 1 (as modified) which survives cancelation and will appear in the overall reaction. To help illustrate this, I will write 2O2 as O2 + O2.
(target reaction) 2C(gr) + O2(g) ----------> 2CO(g) DH = ?
2 x (reaction 1) 2C(gr) + O2(g)
+ O2(g)
----------> 2CO2(g)
DH = -787.0 kJ
(reverse reaction 2) 2CO2(g)
----------> 2CO(g) + O2(g)
DH = +566.0 kJ
Now add together the two given reactions (as modified). This involves bringing down in the total (which I call the net reaction, since it is the net effect of the two reactions) everything not shown in color. (The things in color have been canceled out).
2 x (reaction 1) 2C(gr) + O2(g)
+ O2(g)
----------> 2CO2(g)
DH = -787.0 kJ
(reverse reaction 2) 2CO2(g)
----------> 2CO(g) + O2(g)
DH = +566.0 kJ
________________________________________________________________________
(net reaction) 2C(gr) + O2(g) ----------> 2CO(g) DH = -221.0 kJ
Since the two reactions (as modified) add up to give the target reaction,
their DH values must likewise add up to give
the DH of the target reaction. This is
Hess's Law. Thus, it has been possible to calculate the DH
of a reaction without actually measuring it.