Introduction

1. Combination reactions

 
2. Decomposition reactions

 
3. Displacement reactions (Single replacement)

 
4. Metathesis reactions (Double replacement)

 
5. Combustion reactions

Combination Reactions

8Fe(s)   +   S₈(s)   ---------->   8FeS(s)

2Na(s)   +   Cl₂(g)   --------->   2NaCl(s)

HCl(g)   +   NH₃(g)   ---------->   NH₄Cl(s)

CaO(s)   +   H₂O(l)   +   2CO₂(g)   ---------->   Ca(HCO₃)₂(s)
 

Decompositon Reactions

CaCO₃(s)   ---------->   CaO(s)   +   CO₂(g)

C₁₂H₂₂O₁₁(s)   ---------->   12C(s)   +   11H₂O(g)

4NaHSO₃(s)   ---------->   S(s)   +   SO₂(g)   +   2H₂O(g)   +   2Na₂SO₄(g)

Displacement Reactions

Zn(s)   +   CuSO₄(aq)   ---------->   ZnSO₄(aq)   +   Cu(s)

3Mg(s)   +   2AlCl₃(aq)   ---------->   3MgCl₂(aq)   +   2Al(s)

Ni(s)   +   2AgNO₃(aq)   ---------->   Ni(NO₃)₂(aq)   +   2Ag(s)

However, there are also reactions where non-metals are involved in the displacement.  Examples are

2KBr(aq)   +   Cl₂(aq)   ---------->   2KCl(aq)   +   Br₂(aq)

2NaI(aq)   +   Br₂(aq)   ---------->   2NaBr(aq)   +   I₂(aq)

Metathesis Reactions

sodium                      calcium                              sodium                  calcium
                   +                                 ----->                           +
carbonate                  chloride                             chloride                 carbonate

Na₂CO₃(aq)   +         CaCl₂(aq)   ---------->   2NaCl(aq)   +         CaCO₃(s)
 

barium                       potassium                         barium                     potassium
                     +                               ----->                            +
bromide                     phosphate                        phosphate                bromide

3BaBr₂(aq)   +            2K₃PO₄(aq)   -------->    Ba₃(PO₄)₂(s)   +     6KBr(aq)
 

sodium                       aluminum                          sodium                     aluminum
                   +                                -------->                        +
phosphate                   chloride                           chloride                    phosphate

Na₃PO₄(aq)   +            AlCl₃(aq)    -------->      3NaCl(aq)    +        AlPO₄(s)
 

Combustion Reactions

2C₂H₂(g)   +   5O₂(g)   ---------->   4CO₂(g)   +   2H₂O(g)

CH₄(g)   +   2O₂(g)   ---------->   CO₂(g)   +   2H₂O(g)

2CH₃OH(l)   +   3O₂(g)   ---------->   2CO₂(g)   +   4H₂O(g)

C₂H₅OH(l)   +   3O₂(g)   ---------->   2CO₂(g)   +   3H₂O(g)

In the last 2 reactions, you may be wondering why I wrote CH₃OH rather than CH₄O and C₂H₅OH rather than C₂H₆O.  These molecules are usually represented as I have indicated in order to convey information about the molecular structure.  CH₃ is a methyl group, C₂H₅ is an ethyl group and OH is a hydroxyl group.  C₂H₅OH is sometimes even further expanded and written as CH₃CH₂OH.  The molecular structures are shown below:

          Methyl alcohol                        Ethyl alcohol
 

Dissociation of Ionic Compounds

Ionic compounds typically have high melting points.  At room temperature they exist as solid crystals in which the positive ions are surrounded by negative ions and the negative ions are surrounded by positive ions.  In a crystal of an ionic compound, there is a three dimensional arrangement of ions in a repeating pattern that we call the "crystal lattice".  The arrangement is such that attractive interactions are maximized while repulsive interactions are minimized.  The strong attraction between ions of opposite charge is responsible for the high melting points of these compounds.  Table salt (NaCl), for example, melts at 801 ^oC.  For comparison, "room temperature" is typically considered to be 25 ^oC and water boils (under normal pressure) at 100 ^oC.  In general chemistry, we usually don't work with temperatures high enough to melt ionic compounds, so encountering them as liquids is rare.  We do, however, often work with aqueous (water) solutions of them.  So while we are not likely to deal with NaCl(l), it will not be unusual to have NaCl(aq).

When ionic compounds dissolve in water, the crystal lattice "falls apart" and the ions go their separate ways as they enter the water.  We call this dissociation.  Not all ionic compounds dissolve in water, but those that do dissociate.  Sodium chloride does not dissolve as NaCl formula units -- rather, it dissolves as isolated sodium ions and chloride ions.  We can represent the dissociation of NaCl by the following chemical equation:

                  H₂O
NaCl(s)   ---------->   Na⁺(aq)   +   Cl^-(aq)

Likewise, we can represent the dissociation of calcium bromide by the following equation:

                   H₂O
CaBr₂(s)   ---------->   Ca²⁺(aq)   +   2Br^-(aq)

Water is written above the arrow to indicate that it serves as a catalyst for the process.

There are a couple of student errors I see quite regularly in writing the dissociation equation for CaBr₂.  They are:

                   H₂O
CaBr₂(s)   ---------->   Ca²⁺(aq)   +   Br₂^-(aq)       <=====  WRONG!

and

CaBr₂(s)   ---------->   Ca²⁺(aq)   +   Br₂^2-(aq)     <=====  WRONG!

To avoid mistakes like this, I always tell my students to remember the following phrase:

DON'T INVENT POLYATOMIC IONS

Table 2.4 (on page 56 of your Hill and Petrucci textbook)  lists the common polyatomic ions you will encounter in general chemistry.  If you write a polyatomic ion that is not listed in this table, chances are you are writing an ion that does not exist.  Normally, you should only write monatomic ions and those polyatomic ions that are listed in Table 2.4.  There is no Br₂^- or Br₂^2- ion shown in Table 2.4.  There is no "dibromide" ion of any kind.  Therefore, you can only show the bromine atoms as monatomic bromide ions.  A coefficient of 2 is placed in front of the Br^- ion to balance the equation.  We must account for both bromine atoms in CaBr₂.

Even though sodium chloride does not dissolve as intact formula units, we still sometimes write NaCl(aq).  But we must remember that NaCl(aq) is really Na⁺(aq) + Cl^-(aq).  There are times when it is convenient to represent ionic compounds in "molecular form" (that is, as complete formulas rather than separated ions) even though that's not the way they exist in aqueous solution.  We might want to do this when we need to do stoichiometric calculations on an equation, for example.  The reason for this is, we usually weigh out the chemicals as solids and then dissolve them in water to make the solutions.  If you want to calculate how many grams of one chemical you need to make a certain mass of another, it is easier to do the calculation if the complete formulas are used in the equation -- that's how you weighed the chemicals out when they were still in solid form.

Ionic and Net Ionic Equations -- Application to Displacement Reactions

Zn(s)   +   CuSO₄(aq)   ---------->   ZnSO₄(aq)   +   Cu(s)

Chemists sometimes call this the "molecular" equation, because the copper(II) sulfate and zinc sulfate are written as single formulas as if they were molecules.  Of course, we know they are not, so the term molecular equation is misleading.  Your textbook (Hill and Petrucci) refers to an equation like that above as a complete formula equation.  In the above reaction, we know the CuSO₄ and ZnSO₄ really exist as separated ions.  Therefore, we can write an ionic equation for this reaction as follows:

Zn(s) + Cu²⁺(aq) + SO₄^2-(aq) ----------> Zn²⁺(aq) + SO₄^2-(aq) + Cu(s)

This equation represents the chemical system as it really exists.  It also shows that one of the ions really doesn't participate in the reaction.  Notice that the sulfate ion (SO₄^2-) is present in solution both before (left side of arrow) and after (right side of arrow) the reaction.  When one or more ions appear on both sides of the ionic equation we can cancel them and write a net ionic equation.  From the above ionic equation, we can write the following net ionic equation:

Zn(s)   +   Cu²⁺(aq)   ---------->   Zn²⁺(aq)   +   Cu(s)

Ions like SO₄^2-, which can be cancelled out of the ionic equation, are called spectator ions.  The origin of the term is that these ions really don't participate in the reaction, much as a spectator does not participate at a sporting event.

Thus, when a piece of zinc metal is dropped into a solution of copper(II) sulfate, the actual reaction is between the zinc metal and the Cu²⁺ ions in solution.  The SO₄^2- ions simply drift around in the solution and "watch" what is happening without actually doing anything.  This is seen in Figure 1.  On the left is seen a beaker containing an aqueous solution of CuSO₄.  The CuSO₄ exists in solution as separated Cu²⁺ ions and SO₄^2- ions.  In the middle, a piece of Zn metal has been dropped into the beaker.  A reaction occurs in which Zn atoms leave the solid metal and enter the solution as Zn²⁺ ions.  In order for a Zn atom to become a Zn²⁺ ion, it must lose 2 electrons.  These 2 electrons are given to a Cu²⁺ ion in the solution, causing it to become a neutral Cu atom.  Thus, for each Zn atom that enters the solution as a Zn²⁺ ion, a Cu²⁺ ion is removed from the solution as a neutral Cu atom.  In this way, the total amount of positive charge in the solution remains constant.  The solid piece of zinc "disintegrates" as its atoms enter the solution as ions.  However, the Cu atoms that are formed in the reaction assemble into a mass of solid copper.  Basically, the Zn atoms and the Cu atoms simply switch roles.  The result of the reaction is seen in the beaker on the right side of the diagram.  We say the zinc has displaced the copper from the compound.  Notice that the SO₄^2- ions, although present during the reaction, really didn't do anything.  The only significance of the SO₄^2- is that their negative charge cancels out the positive charge of the Cu²⁺ and Zn²⁺ ions so that overall, the solution is electrically neutral.

Displacement reactions are REDOX reactions.  REDOX is an abbreviation for REDuction-OXidation.  Interestingly, when we say the whole words, we usually switch the order and say "oxidation-reduction".  But REDOX sounds better than OXRED, don't you think?

Oxidation is the loss of electrons and reduction is the gain of electrons.  In the reaction between Zn and CuSO₄, the Zn atoms are losing electrons, which means the element zinc is being oxidized.  At the same time, the Cu²⁺ ions are gaining electrons, which means the element copper is being reduced.  We can see this by looking at the net ionic equation for the reaction and counting the electrons in each atom and ion.

Zn(s)       +       Cu²⁺(aq)     ----->       Zn²⁺(aq)       +       Cu(s)

30 electrons       27 electrons               28 electrons            29 electrons

The number of electrons for each species in the above equation was determined by noting that for neutral atoms, the number of electrons must be equal to the number of protons (atomic number) and for 2+ ions, the number of electrons must be 2 less than the number of protons.

Zinc starts out having 30 electrons and ends up with 28 -- a loss of 2 electrons.  Copper starts out having 27 electrons and ends up with 29 -- a gain of 2 electrons.  There is literally a transfer of electrons from zinc to copper.

Oxidation and reduction reactions always go hand-in-hand.  Free electrons never appear in chemical reactions, so for something to lose electrons, something else must gain them.  The situation is somewhat like the giving and receiving of a gift.  I can't give you a gift unless you are willing to accept it.  Likewise, you can't receive a gift from me unless I am willing to give you one.

Even though oxidation and reduction reactions must always occur together, that does not mean that the oxidation of zinc must always be accompanied by the reduction of copper.  There are numerous oxidation reactions and numerous reduction reactions that take place in chemistry, and the only requirement is that any given oxidation reaction -- in order to occur -- must be accompanied by some reduction reaction.  There are several other reduction reactions with which the oxidation of zinc could be paired.

Although an oxidation or reduction reaction can not be made to take place in the absence of its complementary reaction, we sometimes do split up the reactions on paper and consider the oxidation and reduction reactions separately.  When we do this, we refer to them as half reactions to remind us that when we consider either an oxidation alone or reduction alone, we are only looking at half the picture.  There can't be a reaction unless we have the other half.

The reaction

Zn(s)   +   Cu²⁺(aq)   ---------->   Zn²⁺(aq)   +   Cu(s)

can be split on paper into the following two half reactions:

Zn(s)   ---------->   Zn²⁺(aq)   +   2e^-            (oxidation half reaction)

Cu²⁺(aq)   +   2e^-   ---------->   Cu(s)           (reduction half reaction)

When these two halves are added together, the two electrons (2e^-) cancel out because they appear as a reactant in one equation and as a product in the other.  The result is simply our original net ionic equation.

Since oxidation and reduction reactions must always occur together, why would anyone want to separate them into half reactions?  There are two good reasons.

First, even though an oxidation must always be accompanied by a reduction, they don't have to occur at the same location in space.  For the reaction between Zn and Cu²⁺ described in Figure 1, the reaction takes place at the interface between the zinc surface and the solution.  With this set-up, it is not possible to harness the transfer of electrons between the zinc and the copper.  It is possible, however, to devise a set-up where the oxidation and reduction halves take place in separate locations.  We then create a path through which the electrons lost in oxidation can travel to the location where they will be gained in reduction.  So what we will have is a bunch of electrons flowing along a path from where an oxidation is taking place to where a reduction is taking place.  What do we call flowing electrons?  An electric current!  In other words, I am talking about a battery.  Batteries work by running an oxidation and a reduction at different locations in space.  The oxidation half reaction occurs at the negative pole of the battery, and serves as the source of electrons that are generated there.  After the electrons have traveled through the external circuit (examples: flashlight, portable radio, calculator) they arrive at the positive pole, where they are gained in the reduction reaction.

A second reason for splitting up a REDOX reaction into two halves is to help balance it.  As an example, consider the following REDOX reaction, presented in net ionic form:

Sn⁴⁺(aq)   +   Fe²⁺(aq)   ---------->   Sn²⁺(aq)   +   Fe³⁺(aq)

Is this equation balanced?  If we look only at the atom count, it is.  There is one Sn atom on both sides of the equation, and also one Fe atom on both sides.  But if we look at the electric charges, we find a flaw.  The total charge on the left hand side is 6⁺ (4⁺ + 2⁺ = 6⁺).  The total charge on the right hand side is 5⁺ (2⁺ + 3⁺ = 5⁺).  It is not enough just to have atoms balanced -- electric charges must balance also.  We sometimes find it helpful to split the overall reaction into its oxidation and reduction halves to see how to balance it.  Looking at the Sn, we see it goes from a charge of ⁴⁺ to a charge of 2⁺.  This means it must have gained 2 electrons, to cancel out 2 of the original 4 positive charges.  Looking at Fe, we see it goes from a charge of 2⁺ to a charge of 3⁺.  This means it must have lost 1 electron, to leave an additional proton charge un-neutralized.  Our half reactions are therefore, the following:

REDuction:        Sn⁴⁺(aq)   +   2e^-   ---------->   Sn²⁺(aq)

OXidation:         Fe²⁺(aq)   ---------->   Fe³⁺(aq)   +   e^-

Notice that the reduction reaction requires 2 electrons, but the oxidation reaction only provides 1 electron.  This means the oxidation reaction must occur twice (to provide 2 electrons) every time the reduction reaction occurs once (to use 2 electrons).  Free electrons never appear in the overall reaction, so the number of electrons given off in oxidation must be equal to the number consumed in reduction.  We must therefore, multiply the the oxidation by 2  Our pair of reactions now looks like this:

REDuction:        Sn⁴⁺(aq)   +   2e^-   ---------->   Sn²⁺(aq)

OXidation:         2Fe²⁺(aq)   ---------->   2Fe³⁺(aq)   +   2e^-

When these are added to reconstruct the overall reaction, the 2e^- cancels out, because it is both a reactant and a product.  Bringing down the remaining reactants and products (from both equations), we have

Overall:               Sn⁴⁺(aq)   +   2Fe²⁺(aq)   ---------->   Sn²⁺(aq)   +   2Fe³⁺(aq)

The above equation is balanced.  It has one Sn atom and 2 Fe atoms on each side, and a charge of 8⁺ on each side.  On the left side, the charge arises as 4⁺ + 2 ^. 2⁺ = 4⁺ + 4⁺ = 8⁺ and on the right side, it arises as 2⁺ + 2 ^. 3⁺ = 2⁺ + 6⁺ = 8⁺.
 

Ionic and Net Ionic Equations -- Application to Metathesis Reactions

sodium                      calcium                              sodium                  calcium
                   +                                 ----->                           +
carbonate                  chloride                             chloride                 carbonate

Na₂CO₃(aq)   +         CaCl₂(aq)   ---------->   2NaCl(aq)   +         CaCO₃(s)

Repeated above for you is the word equation and "molecular" equation for the reaction.  We know that ionic compounds dissociate when they dissolve in water, so everything with an (aq) phase label actually exists in water as separated ions, rather than intact formula units.  With this in mind, we can write the following ionic equation.

2Na⁺(aq) + CO₃^2-(aq) + Ca²⁺(aq) + 2Cl^-(aq) ---------->   2Na⁺(aq) + 2Cl^-(aq) + CaCO₃(s)

CaCO₃ has not been split because it is a solid.  In the solid, the ions are in close proximity to each other in the crystal lattice.  Notice that the Na⁺ ions and the Cl^- ions appear in equal numbers on both sides of the equation.  These are our spectator ions for this reaction.  We can cancel these out, and write down what it left.  This will leave the net ionic equation, which is

Ca²⁺(aq)   +   CO₃^2-(aq)   ---------->   CaCO₃(s)

This shows that the actual reaction is between the calcium ions and the carbonate ions.  The sodium ions and chloride ions don't really participate in the reaction.  Because calcium ions and carbonate ions have this reaction in water, we see now that ANY water soluble ionic compound containing the calcium ion will react with ANY water soluble ionic compound containing the carbonate ion to form calcium carbonate.  For example, mixing aqueous solutions of ammonium carbonate and calcium bromide would also lead to the formation of solid calcium carbonate.

ammonium                     calcium                              ammonium                  calcium
                       +                                 ----->                                +
carbonate                      bromide                             bromide                      carbonate

(NH₄)₂CO₃(aq)    +     CaBr₂(aq)   ---------->       2NH₄Br(aq)    +         CaCO₃(s)

2NH₄⁺(aq) + CO₃^2-(aq) + Ca²⁺(aq) + 2Br^-(aq) ---------->   2NH₄⁺(aq) + 2Br^-(aq) + CaCO₃(s)

Ca²⁺(aq)   +   CO₃^2-(aq)   ---------->   CaCO₃(s)

In the above reaction, ammonium ions and bromide ions are the spectator ions.  After crossing out the spectator ions, the CO₃^2- ion appears before the Ca²⁺ ion, but I have reversed the order because it is customary to list the positive ion first.  However, it really makes no difference in what order the reactants are listed -- it is still the same reaction.  I followed this same custom in working out the previous reaction -- with sodium carbonate and calcium chloride.

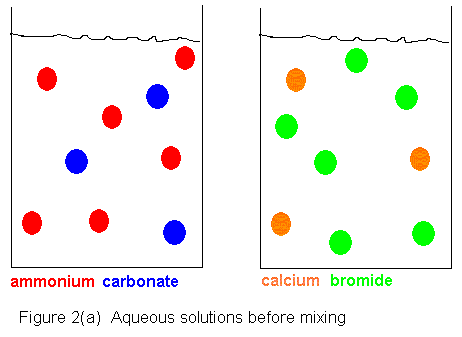
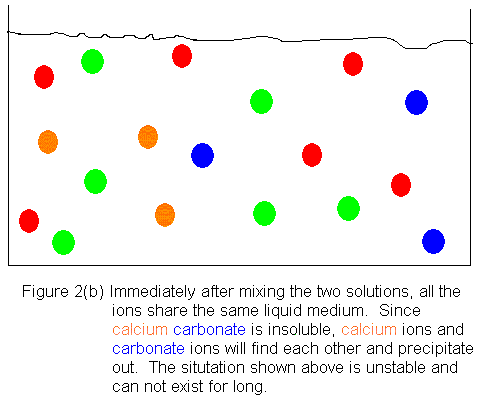
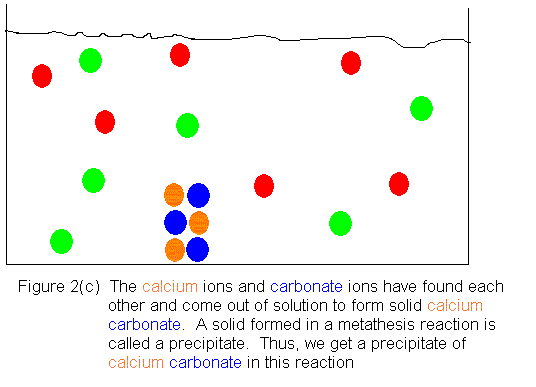
Shown below is an ionic picture of the ammonium carbonate / calcium bromide reaction.  It shows that the ammonium and bromide ions never really do anything.  The only thing that has happened to them is that they used to be in separate containers, and when the solutions are combined, they find themselves in the same container.  On the other hand, the calcium and carbonate ions assemble to form a solid crystal.  The only thing that kept them from reacting before was that they were in separate containers.  As soon as they shared a common aqueous medium, they immediately began assembling to form the solid.  In this reaction, then, we get a precipitate of calcium carbonate, and the supernatant liquid contains dissolved ammonium bromide.



Sometimes, when working on "molecular" or complete formula equations, we might complete a metathesis reaction where no reaction actually occurs.  The complete formula equation can be deceptive, leading us to see a reaction where there is none.  If there is any doubt, we should attempt to work out the net ionic equation for our proposed reaction.  If one can not be written, there is no reaction.  In this case, we should go back to the complete formula equation and write "NR" (for "No Reaction") after the arrow.  The following example illustrates this point.

Example:

Solution:

sodium                          potassium                              sodium                 potassium
                       +                                 ----->                                +
phosphate                      nitrate                                    nitrate                 phosphate

Our next task is to write a chemical reaction using formulas, that correctly conveys the information in the above word equation.  If we merely replace each chemical name with its correct chemical formula we get the following equation.

Na₃PO₄           +           KNO₃         ----->                NaNO₃     +          K₃PO₄

Notice that when we first replace each chemical name with its corresponding chemical formula, we often don't get a balanced equation.  In the above, we have 3 Na atoms on the left but only 1 on the right.  We can solve this problem by putting a coefficient of 3 in front of NaNO₃.  We have 3 K atoms on the right but only 1 on the left.  We can solve this problem by putting a coefficient of 3 in front of KNO₃.  The balanced equation is therefore

Na₃PO₄           +           3KNO₃         ----->                 3NaNO₃     +          K₃PO₄

Next, we need to decide what the phase labels are for the substances shown in the reaction.  The problem has already given away, the fact that sodium phosphate and potassium nitrate are soluble in water, because we are supposed to be mixing aqueous solutions of them, which we could not have if they were not soluble.  However, the sodium nitrate and potassium phosphate are formed in the reaction, and it is possible that one of these is not soluble in water.  Fortunately, there are some rules we can go by to help us decide if a particular ionic compound is soluble in water.  These rules are summarized in tables in most general chemistry textbooks.  In General Chemistry, An Integrated Approach,  Second Edition (1999), the book in use at Palo Alto at the time these notes were written, the table we need appears on page 149.  This table (Table 4.3) shows that all ionic compounds containing group 1A metals are soluble in water.  Since both sodium and potassium are group 1A metals (see the periodic table), we predict that sodium nitrate and potassium phosphate are water soluble, as are sodium phosphate and potassium nitrate.  Hence, all substances in the equation will bear the (aq) label.  Our complete formula equation now looks like this:

Na₃PO₄(aq)     +     3KNO₃(aq)      ----->         3NaNO₃(aq)    +       K₃PO₄(aq)

Recognizing that ionic compounds dissociate into their constituent ions when they dissolve in water, we now write the following ionic equation:

3Na⁺(aq) + PO₄^3-(aq) + 3K⁺(aq) + 3NO₃^-(aq) -----> 3Na⁺(aq) + 3NO₃^-(aq) + 3K⁺(aq) + PO₄^3-(aq)

In the above ionic equation, every single ion listed appears on both sides, and in equal numbers on the two sides.  Therefore, they are ALL spectator ions, and we can cancel ALL of them out.  The rule for writing the net ionic equation is to cross out the spectator ions in the ionic equation, and then write down those ions that were NOT crossed out.  Because we were able to cross out EVERYTHING, there is nothing left to write down.  Thus, there is no net ionic equation, and therefore, no reaction.  Shown below is an ionic picture of the "reaction" we had proposed.  We start out with the sodium and phosphate ions in one container and the potassium and nitrate ions in a separate container.  When we mix the solutions, nothing happens.  We just get a solution containing all 4 types of ions, because there is no possible pairing of the ions that can lead to a water insoluble compound (precipitate).


Notice that the mixed solutions can still be considered to contain the original sodium phosphate and potassium nitrate, because a sodium phosphate solution is characterized as containing sodium ions and phosphate ions, while a potassium nitrate solution is characterized as containing potassium ions and nitrate ions.  The solution shown in Figure 3(b) satisfies both criteria, thus the original reactants are still present.

Of course, one could use the same argument to say the products of our proposed reaction -- sodium nitrate and potassium phosphate -- are also present.  A sodium nitrate solution should contain sodium ions and nitrate ions; a potassium phosphate solution should contain potassium ions and phosphate ions.  Again, the solution shown in Figure 3(b) satisfies both criteria.

So upon mixing, the solution can be thought of as containing all 4 substances shown in our proposed "molecular" equation.  Still, we don't think of this as a reaction, because in a real reaction, the reactants are consumed as the products are formed.  After the reaction, we have substances that were not present in the beginning, and the substances we started with are not present any more.  You might want to scroll back up and review Figure 2 to convince yourself this is true.

Driving Metathesis Reactions to Completion

Acid / Carbonate Reaction

2HCl(aq)   +   Na₂CO₃(aq)   -----> H₂CO₃(aq)   +   2NaCl(aq)
                                                         carbonic acid

Although both products are written with the (aq) label, the H₂CO₃ would not be split in writing an ionic equation, becasue carbonic acid is a weak acid, which, as you will learn in more detail later, does not ionize very much.  We do split the other substances, however.  Therefore, for the ionic equation we would obtain

2H⁺(aq) + 2Cl^-(aq) + 2Na⁺(aq) + CO₃^2-(aq) -----> H₂CO₃(aq) + 2Na⁺(aq) + 2Cl^-(aq)

Recognizing the Na⁺ ions and Cl^- ions as the spectator ions, we would be left with the following net ionic equation:

2H⁺(aq) + CO₃^2-(aq) -----> H₂CO₃(aq)

This is not the end of the story, however.  Carbonic acid, H₂CO₃, is unstable.  It decomposes into water and carbon dioxide:

H₂CO₃(aq) ------> H₂O(l) + CO₂(g)

Therefore, any time the chemistry would lead us to write H₂CO₃, we usually write it as H₂O + CO₂ instead.  In fact, H₂CO₃ has never been isolated in pure form.  It is known only in aqueous solution, and is basically, just another way of writing CO₂(aq).  Therefore, the "molecular" equation given above could be written

2HCl(aq) + Na₂CO₃(aq) -----> H₂O(l) + CO₂(g) + 2NaCl(aq)

the ionic equation would then be

2H⁺(aq) + 2Cl^-(aq) + 2Na⁺(aq) + CO₃^2-(aq) -----> H₂O(l) + CO₂(g) + 2Na⁺(aq) + 2Cl^-(aq)

and the corresponding net ionic equation would be

2H⁺(aq) + CO₃^2-(aq) -----> H₂O(l) + CO₂(g)

Notice that H₂O and CO₂ are not split into ions, because these are molecular -- not ionic -- compounds.

Acid / Sulfite Reaction

2HCl(aq) + Na₂SO₃(aq) -----> H₂SO₃(aq) + 2NaCl(aq)
                                                  sulfurous acid

Like carbonic acid, sulfurous acid is also a weak acid, and would not be split when writing an ionic equation.  If we were going to leave H₂SO₃ intact (ultamitely, we won't) we would write

2H⁺(aq) + 2Cl^-(aq) + 2Na⁺(aq) + SO₃^2-(aq) -----> H₂SO₃(aq) + 2Na⁺(aq) + 2Cl^-(aq)

from which we would get the net ionic equation

2H⁺(aq) + SO₃^2-(aq) -----> H₂SO₃(aq)

However, sulfurous acid is unstable, and decomposes as follows:

H₂SO₃(aq) -----> H₂O(l) + SO₂(g)

Therefore, any time the chemistry would lead us to write H₂SO₃, we usually write is as H₂O + SO₂ instead.  With this in mind, our "molecular", ionic, and net ionic equations become

2HCl(aq) + Na₂SO₃(aq) -----> H₂O(l) + SO₂(g) + 2NaCl(aq)

2H⁺(aq) + 2Cl^-(aq) + 2Na⁺(aq) + SO₃^2-(aq) -----> H₂O(l) + SO₂(g) + 2Na⁺(aq) + 2Cl^-(aq)

2H⁺(aq) + SO₃^2- -----> H₂O(l) + SO₂(g)
 

Acid / Sulfide Reaction

2HCl(aq) + Na₂S(aq) -----> H₂S(g) + 2NaCl(aq)

The H₂S is a molecular compound and is therefore not split when writing the ionic equation.  The other substances are split, however.  The ionic equation is

2H⁺(aq) + 2Cl^-(aq) + 2Na⁺(aq) + S^2-(aq) -----> H₂S(g) + 2Na⁺(aq) + 2Cl^-(aq)

and after removing the spectator ions, Na⁺ and Cl^-, the net ionic equation is

2H⁺(aq) + S^2-(aq) -----> H₂S(g)
 

Reactions With a Solid Reactant

For example, calcium carbonate, CaCO₃ is insoluble in water, but will dissolve in an aqueous hydrochloric acid solution, because the acid converts the insoluble calcium carbonate into calcium chloride, CaCl₂, which is soluble.  The reaction is a metatheis followed by a decompositon of the H₂CO₃ formed in the metathesis.  The metathesis reaction is

CaCO₃(s) + 2HCl(aq) -----> H₂CO₃(aq) + CaCl₂(aq)

This is followed by the decomposition of the H₂CO₃

H₂CO₃(aq) -----> H₂O(l) + CO₂(g)

As discussed earlier, we can simply replace H₂CO₃ with H₂O + CO₂ and write the metathesis reaction as

CaCO₃(s) + 2HCl(aq) -----> H₂O(l) + CO₂(g) + CaCl₂(aq)

In writing the ionic equation for the above "molecular" equation, only the substances with the (aq) label are split into ions.  The CaCO₃ is in solid form, so its ions are in close proximity in the crystal lattace.  The H₂O and CO₂ are not split because they are molecular -- not ionic -- compounds.  The ionic equation is

CaCO₃(s) + 2H⁺(aq) + 2Cl^-(aq) -----> H₂O(l) + CO₂(g) + Ca²⁺(aq) + 2Cl^-(aq)

Only the Cl^- is a spectator ion here.  The net ionic equation is

CaCO₃(s) + 2H⁺(aq) -----> H₂O(l) + CO₂(g) + Ca²⁺(aq)

Even though this reaction occurs by ionizing a previously unionized substance (converting the insoluble substance CaCO₃ into the soluble substance CaCl₂) the net effect is still to decrease the number of ions in solution.  In the above net ionic equation, 2 moles of ions are replaced with only 1 mole of ions.

Reactions That Increase the Number of Ions in Solution

HC₂H₃O₂(aq) + NH₃(aq) -----> NH₄C₂H₃O₂(aq)

In writing the ionic equation for this reaction, we don't split HC₂H₃O₂ because it is a weak acid, and we don't split NH₃ because it is a weak base.  However, NH₄C₂H₃O₂ is a water soluble ionic compound, and is therefore split into ions.  The ionic equation is therefore

HC₂H₃O₂(aq) + NH₃(aq) -----> NH₄⁺(aq) + C₂H₃O₂^-(aq)

Notice there are no spectator ions in this equation.  There is still a net ionic equation, but it is identical to the ionic equation we just wrote.  Recall that you get the net ionic equation by crossing out the spectator ions, and then writing down everything you did NOT cross out.  Here, we crossed out nothing, so we write down EVERYTHING.  The net ionic equation is

HC₂H₃O₂(aq) + NH₃(aq) -----> NH₄⁺(aq) + C₂H₃O₂^-(aq)

Earlier, we saw a situation where a net ionic equation did not exist.  Now we see one where it exists, but it is identical to the ionic equation.  These two cases are at opposite ends of the spectrum, and it is important to know in which case each event occurs:
 

• If there are NO spectator ions, the net ionic equation will exist, but it will be identical to the ionic equation
  
  
• If ALL the ions are spectator ions, the net ionic equation will not exist  (No Reaction)

Acid / Base Chemistry

Acids -- What Are They?

The Arrhenius definition describes an acid as a substance that produces H⁺ ions when dissolved in water.  An acid can be either strong or weak.  A strong acid is one that is 100% ionized when dissolved in water.  That is, the ions formed from the acid do not reassemble to form the molecular acid again.  A weak acid also ionizes in water, but the ions it produces can reassemble to form the molecular acid again.  As a result, only a small fraction of the acid molecules are ionized at any given time.  If you have two solutions of equal concentration -- one of a strong acid and one of a weak acid, the solution of the strong acid will be more acidic.  All of its H⁺ ions are released as free ions into the solution, but with the weak acid, the majority of the H⁺ ions are held by the acid, rather than being released to the solution.  Examples of strong acids are hydrochloric acid and nitric acid.

               H₂O
HCl(g)   ---------->   H⁺(aq)   +   Cl^-(aq)
 

                  H₂O
HNO₃(l)   ---------->   H⁺(aq)   +   NO₃^-(aq)

Examples of weak acids are hydrofluoric acid and nitrous acid.

                H₂O
HF(g)   <---------->   H⁺(aq)   +   F^-(aq)