Chemical kinetics is the study of rates of chemical reactions. When we look at the chemical reactions around us, we find everything from interminably slow to lightening fast. The rusting of an iron nail, or the rotting of a wooden fence can take years to complete, while the explosion of a firecracker takes place in the blink of an eye. The goal of chemical kinetics is to understand the factors that control the rates of chemical reactions.
Why study kinetics? Two important reasons immediately come to mind. First, studying how the rate of a chemical reaction changes under varying conditions often gives a clue as to how the reaction takes place. When we study reaction mechanisms later in these notes, we will see how the dependence of reaction rate on concentration can help us accept or reject a proposed reaction mechanism. Another reason for studying kinetics is that by understanding the factors that control reaction rates, we may be able to improve chemical syntheses by accelerating desirable reactions while minimizing the effects of undesirable reactions.
Reaction rates are affected by the following factors: concentration (for substances in solution or for gases), pressure (for gases), surface area, nature of the reactants, temperature, and presence or absence of a catalyst. Let us briefly look at each of these factors individually.
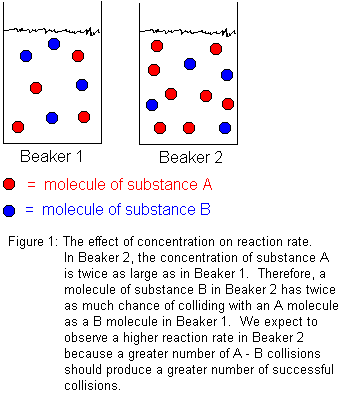
In general, increasing reactant concentrations increases the reaction rate. This is because molecules must collide in order to react. The more concentrated the reactants, the greater the number of molecules in any given volume, and therefore, the greater the number of molecular collisions. Not every molecular collision between reactant molecules will lead to reaction, but some fraction of them will. Certainly, increasing the total number of molecular collisions will increase the number of successful collisions. We define "successful collisions" as those which lead to chemical reaction.

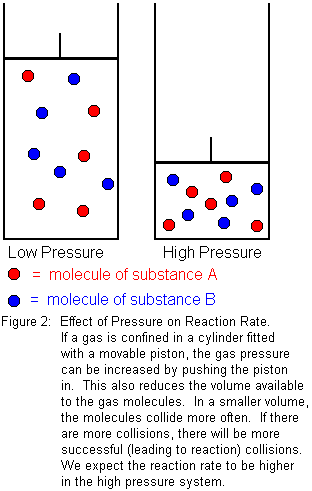
If the substances involved in the reaction are gases, pressure will have an effect on reaction rate. For solids and liquids, the effect is negligible, because solids and liquids are essentially incompressible. Gases are readily compressible, however, so pressure acts as a kind of "concentration" for gases. We know from Boyle's law that the volume of a gas decreases as the pressure increases. For a given amount of gas, increasing the pressure means we are forcing the same number of gas molecules to occupy a smaller volume. In the smaller volume, the molecules will collide more often, which means there will be a greater number of successful (leading to reaction) collisions in a given period of time. We expect reaction rate to increase with pressure.
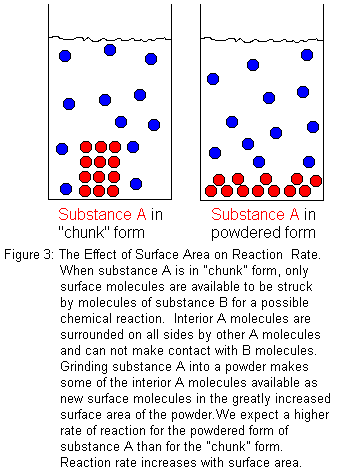
If a chemical reaction takes place at a boundary between two phases, the surface area will affect the reaction rate. When we consider surface area, we are usually thinking of a solid reactant in contact with a liquid solution that contains another reactant. Certainly, other cases are possible. The solid could be reacting with a pure liquid or a gas, but the preceding description is the most common -- especially in undergraduate chemistry courses. So for illustration, let us consider the case of a solid "substance A" that reacts with an aqueous solution of "substance B". We want to compare the reaction rate when an intact "chunk" of substance A and a powdered form of substance A each react with substance B in solution. Since only the molecules at the surface of the solid are available to react, increasing the surface area increases the number of molecules available to react. With a larger surface area, there will be more molecular collisions that potentially could lead to reaction. Therefore, there will be more successful collisions in a given period of time, and we will observe a higher reaction rate. In general chemistry laboratories, this is often demonstrated by comparing the reaction rates for solid sticks of chalk (calcium carbonate, CaCO3) and powdered chalk when dropped into an acid solution, such as hydrochloric acid (HCl).
Some substances are just naturally more reactive than others. Consider, for example, the three metals magnesium (Mg), zinc (Zn), and copper (Cu). If each of these metals is dropped into a concentrated hydrochloric acid solution in a separate test tube, three very different results are obtained. The magnesium is consumed within seconds, the zinc is consumed but takes considerably longer, and the copper shows no reaction. The chemical equations for these reactions (hypothetical in the case of copper) are all very similar. In each case, the metal is oxidized to the divalent cation and the hydrogen ion (H+) from the acid is reduced to molecular hydrogen gas.
For magnesium:
Complete Formula Equation: Mg(s) + 2HCl(aq) ----------> MgCl2(aq) + H2(g)
Net Ionic Equation: Mg(s) + 2H+(aq) ----------> Mg2+(aq) + H2(g)
For zinc:
Complete Formula Equation: Zn(s) + 2HCl(aq) ----------> ZnCl2(aq) + H2(g)
Net Ionic Equation: Zn(s) + 2H+(aq) ----------> Zn2+(aq) + H2(g)
For copper
Complete Formula Equation: Cu(s) + 2HCl(aq) -----X-----> CuCl2(aq) + H2(g)
Net Ionic Equation: Cu(s) + 2H+(aq) -----X-----> Cu2+(aq) + H2(g)
Looking at the complete formula equations, you can see that these are all displacement reactions -- the metal displaces hydrogen from its compound. The net ionic equations show that these are also redox reactions. The metal is oxidized, while the hydrogen is reduced. In the above reactions, it is the ease or difficulty of oxidation of the metal that determines the rate of the reaction. Magnesium oxidizes very easily, so it reacts vigorously in concentrated acid solutions. Zinc is more difficult to oxidize, so the reaction rate is slower. Finally, copper is so difficult to oxidize that it will not react in a concentrated HCl solution. Hydrogen has a higher oxidation potential than copper, so the system will remain in the state with the metal in the reduced form and the hydrogen in ionic form (H+). It is possible to oxidize the copper to Cu2+ by using an "oxidizing acid", but in this case, the acid anion, rather than H+, is what gets reduced. Nitric acid, HNO3 is an example of an oxidizing acid.
Complete Formula Equation: Cu(s) + 4HNO3(aq) ----------> Cu(NO3)2(aq) + 2NO2(g) + 2H2O(l)
Net Ionic Equation: Cu(s) + 4H+(aq) + 2NO3-(aq) ----------> Cu2+(aq) + 2NO2(g) + 2H2O(l)
Of course, magnesium and zinc would also react with HNO3 and would react faster than copper because they are more easily oxidized, and because both H+ ions and NO3- ions could serve as oxidizing agents. In the case of copper, only NO3- is strong enough to serve as an oxidizing agent.
Temperature affects the rate of a chemical reaction in two ways. The effect that usually comes to mind first for most chemistry students is molecular velocity. When we looked at the effect of concentration and pressure on reaction rate, we noted that molecules must collide in order to react. Temperature is a measure of the average kinetic energy of the molecules. The higher the temperature, the higher the average kinetic energy. The kinetic energy of a moving object is equal to one half the product of its mass and the square of its velocity, that is,
K.E. = ½ m v2
where m is the mass and v is the velocity. Since the molecules have a fixed mass, an increased kinetic energy means an increased velocity. That is, the molecules are moving faster in a hot system than in a cold one. For a collection of moving molecules in a fixed volume, the molecules will collide more often if they are moving faster. Therefore, one way that increasing the temperature increases reaction rate is by making the molecules collide more often. This is only a minor factor, however.
A second way that increasing the temperature increases reaction rate is through its effect on the collision energy. This is by far, the most important factor in increasing the reaction rate. Every chemical reaction has a characteristic activation energy. The activation energy is the minimum energy that the reacting molecules must bring into the collision in order to react. If they collide with less than this amount of energy, they simply bounce off of each other unchanged. If the average kinetic energy of the molecules is small in comparison to the activation energy, most of the molecular collisions don't lead to reaction. Collisions may be occurring frequently, but most of them are ineffective, so the reaction rate is very low. If the system is heated, the average kinetic energy of the molecules is increased. When the average kinetic energy is comparable to the activation energy, a much greater fraction of the molecules successfully react when they collide. The percentage of successful collisions usually does not reach 100%, even when the average kinetic energy far exceeds the activation energy. This is because the molecules must collide in the correct orientation in order to react. Consider this analogy: You are standing in a room holding a baseball. About 15 feet in front of you is a window. Let's define a "chemical reaction" as the ball breaking through the glass window and landing outside. If you throw the ball gently and it hits the window, it does not break the glass and lands inside the room. The orientation was correct, but there was not sufficient energy, so no "chemical reaction" took place. If you throw the ball very hard, but you miss the window and hit the wall, the glass does not break and the ball lands inside the room. There was sufficient energy, but the orientation was incorrect, so no "chemical reaction" occurred. Finally, suppose you throw the ball very hard and it hits the window. The glass breaks, and the ball lands outside the room. The orientation was correct, and there was sufficient energy, so a "chemical reaction" took place.
It has been noted that temperature's effect on collision energy is far more important than its effect on collision frequency. To see how these two contributions compare in determining reaction rate, consider the following:
It has been said that the "typical" chemical reaction approximately doubles its rate when the temperature is raised by 10 oC. This generalization is usually applied at 25 oC. Thus, for many chemical reactions, we find the rate is approximately twice as fast at 35 oC as it is at 25 oC. How much of the increase is caused by the increased collision frequency and how much by the increased collision energy? Well, by calculations that are beyond the scope of this course, it can be shown that the collision frequency at 35 oC is approximately 3% higher than at 25 oC. But if the reaction rate has doubled, that's a 100% increase in the reaction rate. Only 3% of that can be attributed to the increased collision frequency. The other 97% is caused by the increased collision energy.
A catalyst is a substance that increases the rate of a chemical reaction without being consumed in the reaction. A catalyst may be either homogeneous or heterogeneous.
A homogeneous catalyst is one which is in the same state as the substances in the reaction being catalyzed. For example, hydrogen peroxide, H2O2 in aqueous solution slowly decomposes into water and oxygen:
2H2O2(aq) ----------> 2H2O(l) + O2(aq) (slow)
Unassisted, this reaction is very slow. However, if we add an aqueous solution containing iodide ions (I-), the reaction is much faster.
I-
2H2O2(aq) ----------> 2H2O(l)
+ O2(g)
(fast)
The I- is in aqueous solution, and so is the H2O2 it catalyzes. The catalyst and reactant are in the same state, making the I- a homogeneous catalyst.
A heterogeneous catalyst is in a different state than the substances in the reaction being catalyzed. For example, the hydrogenation of acetylene (C2H2) to form ethylene (C2H4) is catalyzed by a nickel metal surface:
Ni
C2H2(g) + H2(g)
----------> C2H4(g)
Here, a reaction between two gaseous substances is catalyzed by nickel, a solid. The nickel is a heterogeneous catalyst because it is in a different state than the substances whose reaction is being catalyzed.
In neither of the above two cases is the catalyst "used up" by the reaction. Typically, a homogeneous catalyst undergoes some temporary change, but it is always returned at the end of the reaction. A heterogeneous catalyst usually plays a more passive role. For example, the nickel in the above reaction merely provides a surface on which the molecules can "land" (the technical word is adsorb) and encounter each other to react.
A more detailed account of how catalysts work will be presented in a later section of these notes.
When you express the rate of something, you are stating the amount of "progress" that occurs in a given amount of time. For example, if you drive a total distance of 80 miles in 2 hours time, your average rate of travel is 40 miles per hour. In the equation below, the symbol D means "change in".
Ddistance
80
miles
Speed = ----------- =
----------- = 40 miles / hour
D
time
2 hours
Of course, if you drive for two hours, it is unlikely that you will travel at a constant speed for the entire two hours. One way to go 40 miles per hour would be to maintain a constant speed of 40 mph for the entire 2 hour journey, but most likely your speed will change in response to road conditions. You slow down when a car changes lanes in front of you, and you come to a stop at a red light. You speed up when entering a multilane freeway in light traffic, and then slow down again when you exit the freeway. So the driver who travels 80 miles in 2 hours has an average speed of 40 miles / hour, but the actual speed at any moment in time could be more or less than that. The actual speed at any given point in time is the instantaneous speed. It's the speed that is reported by a police radar gun at the split second the officer points the device at your car. It is possible to get a speeding ticket for going 80 miles / hour even when the average speed for your journey is only 40 miles / hour.
Likewise, when we express the rate of a chemical reaction, what we really measure in the laboratory is an average rate over some observation period. The reaction has an instantaneous rate at each point in time, however. If the observation period is very short, the average rate is essentially the same as the instantaneous rate. For example, if a reaction takes about 10 minutes (600 seconds) to complete, and you monitor the reaction over the time interval 120.0 seconds to 120.1 seconds (measured from the start of the reaction), the average rate over that time interval is essentially the same at the instantaneous rate at 120.0 seconds. This is because the duration of the observation period (0.1 seconds) is very short in comparison to the total timescale for the reaction (600 seconds). Given that the reaction takes 600 seconds to complete, very little change is expected in 0.1 seconds, which amounts to only 1/6000 of the total timescale. If the reaction is going to be monitored for a very short period of time (to get an approximation of an instantaneous rate) the most useful time to make the observation is at the beginning of the reaction. We then get what is called the initial rate of the reaction. The initial rate is the instantaneous rate at time zero. What makes this so useful is that we can study a reaction in the forward direction without being concerned about a reverse reaction involving the products. We typically begin with only reactants when studying a reaction. At very early times in the reaction, the product concentrations are very low, so the reverse reaction is negligible. At later times, significant concentrations of products may exist, and if the reaction is reversible, the reverse reaction offsets the forward reaction, making it harder to determine the true rate of conversion of reactants to products.
In section 2.1, we looked at the rate of travel of a car out on a 2 hour drive. But how do we apply these ideas to a chemical reaction? What do we measure to get the rate of a reaction?
A chemical reaction takes one or more substances referred to as reactants and converts them to one or more other substances referred to as products. To determine how fast a reaction is taking place, we record how fast the "amounts" of these substances are changing. But just what do we mean by "amounts"?
The most often reported measure of reaction rate is the amount by which the concentration of something changes in a given amount of time. Concentration is usually expressed in units of moles per liter for this purpose.
As an example, let us return to the iodide ion catalyzed decomposition of H2O2 mentioned earlier:
I-
2H2O2(aq) ----------> 2H2O(l)
+ O2(g)
Because the system is losing oxygen gas, one way to monitor the progress of the reaction is to follow the mass loss of the system over time. The decrease in mass over any time interval is the mass of oxygen that was lost in that time interval.
Suppose we start with 1.00 L of an aqueous solution known to have an H2O2 concentration of 0.882 M and record the following data:
|
TIME (seconds) |
Accumulated O2(g) |
[H2O2] (M) |
|
0 |
0 |
0.882 |
|
60 |
2.960 |
0.697 |
|
120 |
5.056 |
0.566 |
|
180 |
6.784 |
0.458 |
|
240 |
8.160 |
0.372 |
|
300 |
9.344 |
0.298 |
|
360 |
10.336 |
0.236 |
|
420 |
11.104 |
0.188 |
|
480 |
11.680 |
0.152 |
|
540 |
12.192 |
0.120 |
|
600 |
12.608 |
0.094 |
Data from General Chemistry, An Integrated Approach, 2nd Ed., Hill & Petrucci, Prentice Hall, 1999 page 559.
Over the interval 0 to 60 seconds, a total of 2.960 g of O2 is released. The number of moles of O2 is calculated as follows:
1 mol O2
2.960 g O2 x
--------------- = 0.092503 mol O2
31.9988 g O2
From the reaction stoichiometry, we see that 2 moles of H2O2 must decompose to get just 1 mole of O2. Therefore, the number of moles of H2O2 that decomposed is calculated as follows:
2 mol H2O2
0.092503 mol O2 x
-------------- = 0.185006 mol H2O2
1 mol O2
The solution we started with had an H2O2 concentration of 0.882 mol / L and a volume of 1.00 L. So the starting number of moles of H2O2 was
0.882 mol
----------- x 1.00 L = 0.882 mol
1 L
Subtracting the moles of H2O2 that decomposed from the moles originally present should give the number of moles remaining:
0.882 mol - 0.185006 mol = 0.696994 mol
These moles are still present in the 1.00 L of solution volume:
0.696994 mol
--------------- = 0.696994 mol / L
≈ 0.697 mol / L
1.00 L
The other concentrations shown in the table were calculated using the same procedure.
Our next goal is to use the data in the table to calculate the reaction rate. First, however, we need to know something about the conventions that are followed in reporting reaction rates. Not all substances in a chemical equation change their concentrations at the same rate, due to differences in the stoichiometric coefficients in the balanced equation. For example, consider the hypothetical reaction
2A(aq) + B(aq) ----------> 3C(aq) + 2D(aq)
Looking at the above equation, we see that substance A is being consumed twice as fast as substance B. Substance C is being formed at a rate 3 times the rate of removal of substance B and 50% faster than substance D is being formed. As these comparisons show, two chemists could be studying the same reaction and report different rates, depending on which substance they chose to use as the basis for measuring the rate. One way to get around this difficulty is to divide the rate we would otherwise calculate by the coefficient of the substance in question. This gives the same rate for the chemical reaction regardless of which substance we monitor to measure the rate. For the above reaction, all of the following expressions would give the same numerical value:
D[A]
D[B]
D[C]
D[D]
Rate - ------
= - ------ =
------- = -------
2 Dt
Dt
3 Dt
2 Dt
If the substance being monitored is a reactant, we need to include a negative sign in front of the fraction in order to get a positive rate. This is because the change in concentration is a negative number for a reactant. The negative sign placed out front cancels this negative, yielding a positive rate. The change in concentration for the reactants is positive, so no negative sign is needed in front of the fraction.
We can avoid having to divide by the coefficient of the substance used to monitor the rate by balancing the equation in such a way as to make that coefficient equal to one. For example, the reaction
I-
2H2O2(aq) ----------> 2H2O(l)
+ O2(g)
can be re-written in the form
I-
H2O2(aq) ----------> H2O(l)
+ ½O2(g)
in which the rate is expressed as
D[H2O2]
Rate = - -------------
Dt
Let us used the reaction and rate expression just presented to calculate the average rate of the reaction over the time interval 0 to 60 seconds and over the time interval 540 to 600 seconds.
For the interval 0 to 60 seconds, we have the following:
D[H2O2] = [H2O2]final - [H2O2]initial
= 0.697 mol / L - 0.882 mol / L = -0.185 mol / L
Dt = tfinal - tinitial
60 s - 0 s = 60 s
D[H2O2]
-0.185 mol / L
Rate = - ------------- =
- ----------------- = 3.1 x 10-3 mol /
L s
Dt
60 s
For the interval 540 to 600 seconds, we have the following:
D[H2O2] = [H2O2]final - [H2O2]initial
= 0.094 mol / L - 0.120 mol / L = -0.026 mol / L
Dt = tfinal - tinitial
600 s - 540 s = 60 s
D[H2O2]
-0.026 mol / L
Rate = - ------------- =
- ----------------- = 4.3 x 10-4 mol /
L s
Dt
60 s
Notice that the average rate is smaller during the interval 540 to 600 seconds than it is during the interval 0 to 60 seconds. This is consistent with the idea that molecules must collide in order to react. The reaction removes H2O2 molecules from the system by converting them to H2O molecules and O2 molecules. The longer the reaction goes on, the smaller the number of H2O2 molecules in the system. Therefore, the collision frequency between H2O2 molecules decreases as time goes on, and the reaction rate slows down.
Before moving on, a word on units is in order. In calculating the reaction rates, the units mol / L s have been used. However, we could also have expressed the units as M / s, M s-1 or mol L-1 s-1. All of these are equivalent. The symbol M is an abbreviation for mol / L, and we can use an exponent of -1 on something as an alternative way of saying that it appears in the denominator of a fraction. It is important that you become comfortable with all of these alternative forms of expressing the units, so you will be prepared for whatever comes your way.
In Section 2.2, we looked at the decomposition of H2O2 in a solution which had an initial concentration of 0.882 mol / L. We saw how we could use the data in the table to calculate the reaction rate at various times in the reaction. But now suppose we used a different solution, say, one in which the initial concentration of H2O2 was 1.500 mol / L? Would we have to do the experiment all over again to obtain the reaction rates in this new solution? Fortunately, the answer is no. Once we have studied a given reaction at a particular temperature, it is possible to describe the reaction rate with an expression called a rate law. A rate law allows you to plug in any concentrations you wish in the equation and calculate what the reaction rate should be for those concentrations. For most chemical reactions, the rate law is simply the product of a constant, called the rate constant, and the reactant concentrations, each raised to some power. The power often turns out to be an integer, though it does not have to be. That is, a reaction of the form
aA + bB ----------> cC + dD
usually has a rate law of the form
Rate = k [A]x [B]y
where k is the rate constant and x and y are called the orders of reaction. That is, this reaction is "xth order in A" and "yth order in B". The overall order of a reaction is the sum of the individual orders. Thus, this reaction is (x + y)th order overall.
Students are sometimes tempted to conclude that the exponents on the concentrations should be the same as the stoichiometric coefficients in the balanced equation. This is true in the case of an elementary reaction, but is not true in general. An elementary reaction is one that occurs in a single step, exactly as written. But many reactions don't occur that way. The equation that describes the reaction may be the net effect of two or more simpler -- that is, elementary -- reactions. If a reaction is not elementary, there is no necessary relationship between the coefficients in the balanced equation and the exponents in the rate law. They could happen to be the same, but they don't have to be. If a reaction has a rate law with orders that don't match the coefficients in the balanced equation, you know it is not an elementary reaction, because if the reaction was elementary, they would have to match. On the other hand, the fact that a reaction has a rate law with orders that match the coefficients does not prove that it is an elementary reaction. A non-elementary reaction could happen to have orders that match the coefficients. Consider the following analogy: think of an elementary reaction as rain, and think of the match between reaction orders and coefficients as a wet sidewalk. If it is raining, the sidewalk must be wet. However, given that the sidewalk is wet, this does not prove it is raining. The sidewalk could be wet from a poorly adjusted sprinkler. However, it the sidewalk is dry (reaction orders and coefficients do not match), you know for sure it is not raining.
Unless you are told in a problem you are working to treat the reaction as elementary, you should not assume it is elementary. In the absence of some assurance that the reaction is elementary, the only way to obtain the reaction orders is from experimental data. This is most conveniently done by conducting an initial rate study on the reaction, using reactant concentrations that differ by integer multiples from one experiment to the next. For example, consider the following reaction and initial rate data:
2NO(g) + Cl2(g) ----------> 2NOCl(g)
|
Experiment |
Initial [NO] |
Initial [Cl2] |
Initial Rate |
|
1 |
0.0125 mol L-1 |
0.0255 mol L-1 |
2.27 x 10-5 mol L-1 s-1 |
|
2 |
0.0125 mol L-1 |
0.0510 mol L-1 |
4.55 x 10-5 mol L-1 s-1 |
|
3 |
0.0250 mol L-1 |
0.0255 mol L-1 |
9.08 x 10-5 mol L-1 s-1 |
If we now assume the rate law of the reaction has the form
Rate = k [NO]x [Cl2]y
we can substitute data from the table into the equation to determine the reaction orders (x and y) and the rate constant (k). We must determine the reaction orders before we can can find the rate constant. We compare the experiments two at a time, picking two in which one of the reactant concentrations is the same. This allows us to determine the reaction order in the other reactant -- the one for which the concentration is different in the two experiments being compared. To get the reaction order with respect to NO, we can compare experiments 1 and 3. In these two experiments, the same concentration is used for Cl2, but different concentrations are used for NO. Therefore, any difference we see in rates for these two experiments (and we do see a difference) must be attributed to the difference in NO concentration.
Expt. 3: 9.08 x 10-5 mol L-1 s-1 = k (0.0250 mol L-1)x (0.0255 mol L-1)y
Expt. 1: 2.27 x 10-5 mol L-1 s-1 = k (0.0125 mol L-1)x (0.0255 mol L-1)y
If we divide the equation for Expt. 3 by the equation for Expt. 1, we can cancel out the out the power of 10 and the units of rate on the left, and we can cancel out the rate constant and concentration of Cl2 on the right.
9.08 x 10-5 mol L-1 s-1
k (0.0250 mol L-1)x (0.0255 mol L-1)y
------------------------- =
------------------------------------------
2.27 x 10-5 mol L-1 s-1
k (0.0125 mol L-1)x (0.0255 mol L-1)y
After canceling the quantities that appear in both the numerator and denominator in this equation, it reduces to
9.08 (0.0250 mol L-1)x
----- = -------------------
2.27 (0.0125 mol L-1)x
On the right hand side, since the numerator and denominator are raised to the same power (x), we can re-write this as the entire fraction being raised to the power x. Then we don't need to have a separate exponent for the numerator and denominator.
9.08 |---
0.0250 mol L-1 ---| x
----- = |
------------------ |
2.27 |---
0.0125 mol L-1
---|
Since the units mol L-1 are now in a common set of parentheses and in both the numerator, we can cancel them.
9.08 |---
0.0250 ---| x
----- = |
-------- |
2.27 |---
0.0125 ---|
If we simplify the above expression by carrying out the division on each side, we have
4 = (2)x
Since 2 must be squared to get 4, it is clear that x = 2. It will usually be the case in general chemistry problems that the value of the exponent will be obvious at this stage. However, the mathematically rigorous way to solve for the exponent, should you ever need it, is to take the log of both sides.
log 2x = log 4
In addition to taking the log of both sides, the equation has been reversed to put x on the left hand side. Reversing the equation does not change it in a mathematical sense, and has no bearing on the solution. We now use the fact that the log of a number raised to a power is equal to the power multiplied by the log of the original number. This allows us to re-write the left hand side as
x log 2 = log 4
Then dividing both sides by log 2 gives
log
4 0.60206
x = ------- =
---------- = 2
log
2 0.30103
We must avoid the temptation to simply cancel out the word log. In this case, it seems to work, because it leaves us with 4 / 2, which is 2. It just happens to "work" here, but it is not a mathematically sound procedure. Always keep in mind that what we have here is log of 4 and log of 2, not log times 4 and log times 2.
We have now determined that the reaction is second order in NO. Next, let's get the order in Cl2. To do this, we need to compare two experiments in which the concentration of NO is the same but the concentration of Cl2 varies. The two experiments to compare in this case are Expt. 1 and Expt. 2. Again, we substitute the data from the initial rate table into the equation
Rate = k [NO]x [Cl2]y
Here are the substitutions:
Expt. 2: 4.55 x 10-5 mol L-1 s-1 = k (0.0125 mol L-1)x (0.0510 mol L-1)y
Expt. 1: 2.27 x 10-5 mol L-1 s-1 = k (0.0125 mol L-1)x (0.0255 mol L)y
If we divide the equation for Expt. 2 by the equation for Expt. 1, the power of 10 and the rate units cancel out on the left, while the rate constant and concentration of NO cancel out on the right.
4.55 x 10-5 mol L-1 s-1
k (0.0125 mol L-1)x (0.0510 mol L-1)y
------------------------ =
-----------------------------------------
2.27 x 10-5 mol L-1 s-1
k (0.0125 mol L-1)x (0.0255 mol L-1)y
After canceling the quantities that appear in both the numerator and denominator, the equation reduces to
4.55
(0.0510 mol L-1)y
----- = ---------------------
2.27 (0.0255
mol L-1)y
As before, we can "factor out" the exponent, so to speak, and have a fraction that is raised to a single power, rather than separately raising the numerator and denominator to that same power.
4.55 |---
0.0510 mol L-1 ---| y
----- = |
------------------ |
2.27 |---
0.0255 mol L-1
---|
Since the units mol L-1 are now in a common set of parentheses and in both the numerator, we can cancel them.
4.55 |---
0.0510 ---| y
----- = |
-------- |
2.27 |---
0.0255 ---|
If we simplify the above expression by carrying out the division on each side, we have
2 = (2)y
Since any number raised to the first power is equal to itself, it is clear that y = 1. However, we can show this completely by taking the log of both sides, just as we did before:
log 2y = log 2
Then using the fact that the log of a number raised to a power is equal to the power multiplied by the log of the original number, we re-write the left hand side:
y log 2 = log 2
Dividing both sides by log 2, we have
log
2
0.30103
y = ----------- =
----------- = 1
log
2
0.30103
Here, you could just cancel out the entire log 2 because you have the same quantity in the numerator and denominator. But again, you must remember that what you are canceling out is the quantity represented by log 2. You don't "cancel the log and cancel the 2", because this is not log times 2, it is log of 2.
Now the reaction orders have been determined for both reactants. The reaction is second order in NO and first order in Cl2. The reaction is third order overall, because the overall order is the sum of all the individual orders. Since both orders have been determined, we can now calculate the rate constant. The rate law we have so far is
Rate = k [NO]2 [Cl2]
The exponent of 1 on [Cl2] is understood and not written. If we now solve this equation for k, we have
Rate
k = --------------
[NO]2
[Cl2]
We can now use any of the experiments presented in the initial rate table to calculate the rate constant. All of the experiments should yield the same rate constant, at least within acceptable round-off error. Let's calculate the rate constant for all three experiments, just to illustrate this.
2.27 x 10-5 mol L-1 s-1
Expt. 1: k =
--------------------------------------- = 5.70 mol-2
L2 s-1
(0.0125 mol L-1)2 (0.0255 mol L-1)
4.55 x 10-5 mol L-1 s-1
Expt 2: k =
--------------------------------------- = 5.71 mol-2
L2 s-1
(0.0125 mol L-1)2 (0.0510 mol L-1)
9.08 x 10-5 mol L-1 s-1
Expt 3: k =
--------------------------------------- = 5.70 mol-2
L2 s-1
(0.0250 mol L-1)2 (0.0255 mol L-1)
Within acceptable round-off error, we get the same rate constant each time. We can attribute the slight variation in the rate constant for Expt. 2 as being caused by the rate being 4.55 x 10-5 instead of 4.54 x 10-5 which would represent an "exact" doubling of the rate. The concentration of Cl2 is doubled in Expt. 2, as compared to Expt. 1, and it seems more logical that the rate would also double, rather than just slightly more than double. We must remember that physical measurements always have uncertainties. That's why we learned about significant figures in General Chemistry I. Our data in this problem is given to 3 significant figures, and within this limit, the three calculated values are essentially the same. The last digit in a correctly reported value can be off by a unit or two.
Notice that a rate constant has both a numerical value and units associated with it. In this problem, we obtained units of mol-2 L2 s-1, but those are not always the units. The units of mol, L, and time (usually measured in seconds) always appear, but the powers to which they are raised depend on the overall order of the reaction. The pattern is this:
mol1-overall order Loverall order-1 time-1
The reaction considered in this problem was third order overall.
1 - overall order = 1 - 3 = -2
overall order - 1 = 3 - 1 = 2
If you find the pattern easy to remember, you can use that rather than having to grind through the "algebra of units" in the calculation of the rate constant.
In the previous problem, everything has been worked out in full. However, it is usually easy to obtain the reaction orders by inspection, without having to laboriously substitute everything into two equations and then divide one by the other. Most general chemistry problems of this type involve the initial reactant concentrations being changed by integer multiples. When the concentration is multiplied by some factor, the rate is multiplied by that factor raised to the power of the reaction order in that reactant. So if a reactant concentration is doubled and the rate also doubles, the reaction must be first order in that reactant, because 21 = 2. If doubling a reactant concentration causes the reaction rate to quadruple, the reaction is second order in that reactant, because 22 = 4. In General Chemistry II, we usually deal with reaction orders of 0, 1, and 2, and the concentrations are usually multiplied by 2, 3, and perhaps 4 at the most. With this in mind, we can construct the following table showing the effect of increasing the reactant concentration by small integer powers.
|
Concentration Factor |
Order |
Rate Factor |
|
2 |
0 |
1 |
|
3 |
0 |
1 |
|
4 |
0 |
1 |
|
2 |
1 |
2 |
|
3 |
1 |
3 |
|
4 |
1 |
4 |
|
2 |
2 |
4 |
|
3 |
2 |
9 |
|
4 |
2 |
16 |
To use the above table in working a problem, determine the factor by which the concentration is increased, then determine the factor by which the rate increases. Find the row in the table that includes the concentration factor and rate factor. The number in the middle of the row is the reaction order in that reactant. Note that
Concentration FactorOrder = Rate Factor
To illustrate the shortcut to getting reaction orders, consider the following problem:
For the reaction
2HgCl2(aq) + C2O42-(aq) ----------> 2Cl-(aq) + 2CO2(aq) + Hg2Cl2(s)
the following initial rate data is available
|
Experiment |
Initial [HgCl2] |
Initial [C2O42-] |
Initial Rate |
|
1 |
0.105 mol L-1 |
0.15 mol L-1 |
1.8 x 10-5 mol L-1 s-1 |
|
2 |
0.105 mol L-1 |
0.30 mol L-1 |
7.1 x 10-5 mol L-1 s-1 |
|
3 |
0.052 mol L-1 |
0.30 mol L-1 |
3.5 x 10-5 mol L-1 s-1 |
|
4 |
0.052 mol L-1 |
0.15 mol L-1 |
8.9 x 10-6 mol L-1 s-1 |
The rate law is expected to have the form
Rate = k [HgCl2]x [C2O42-]y
where k, x, and y are parameters we must determine. To obtain x, the order of the reaction with respect to HgCl2 we can compare experiments 2 and 3. These two experiments have the same initial concentration of C2O42-, so any difference we see in initial rates must be due to the difference in initial concentrations of HgCl2. Looking at the two concentrations of HgCl2, there is approximately a factor of 2 difference between them. The HgCl2 concentration is 0.052 mol L-1 in experiment 3 and 0.105 mol L-1 in experiment 2. An "exact" doubling would have a HgCl2 concentration of 0.104 mol L-1 in experiment 2. We must remember that physical measurements have uncertainties. It seems reasonable that the experimenter's intent was to double the concentration in experiment 2, as compared with experiment 3. Now lets compare the initial rates in experiments 2 and 3. Since the powers of 10 are the same in both rates (10-5) we only have to compare the mantissas. The mantissa is 7.1 in experiment 2 and 3.5 in experiment 3. This is approximately a factor of 2 difference.
7.1 / 3.5 = 2.03 » 2
Our concentration and rate factor table shows that if the concentration and rate factors are both 2, the order is 1. In fact, anytime the concentration and rate change by the same factor, the order is 1. So just by "eyeballing" the data, we have been able to determine that the reaction is first order in HgCl2.
To get the order with respect to C2O42-, we can compare experiments 1 and 2, which use the same initial concentration of HgCl2 but different initial concentrations of C2O42-. Any difference in initial rates in these two experiments must be solely due to the difference in C2O42-. There is a factor of 2 difference in the C2O42- concentrations (0.30 versus 0.15). In comparing the corresponding reaction rates, we can again ignore the common power of 10. Comparing the mantissas, there is approximately a factor of 4 difference.
7.1 / 1.8 = 3.9 » 4
We will assume that we are acceptably close to the integer 4 within the 2 significant figure limit of precision in these data. We then have a concentration factor of 2 and a rate factor of 4, which implies a reaction order of 2 (see the concentration and rate factor table).
We have determined -- essentially by inspection -- that the reaction is first order in HgCl2 and second order in C2O42-. Only the rate constant (k) remains to be determined. Taking our rate law,
Rate = k [HgCl2] [C2O42-]
and solving it for k, we have
Rate
k = ----------------------
[HgCl2]
[C2O42-]2
We can substitute data from any of the four experiments to calculate the rate constant k. The calculations for all of the experiments should agree on the value of k, within acceptable round-off error.
1.8 x 10-5 mol L-1 s-1
Expt. 1: k =
----------------------------------- = 7.6 x 10-3
mol-2 L2 s-1
(0.105 mol L-1) (0.15 mol L-1)2
7.1 x 10-5 mol L-1 s-1
Expt. 2: k =
---------------------------------- = 7.5 x 10-3
mol-2 L2 s-1
(0.105 mol L-1) (0.30 mol L-1)2
3.5 x 10-5 mol L-1 s-1
Expt. 3: k =
---------------------------------- = 7.5 x 10-3
mol-2 L2 s-1
(0.052 mol L-1) (0.30 mol L-1)2
8.9 x 10-6 mol L-1 s-1
Expt. 4 k =
---------------------------------- = 7.6 x 10-3
mol-2 L2 s-1
(0.052 mol L-1) (0.15 mol L-1)2
The rate constant calculations are consistent within the two significant figure precision of the data.
The rate law expressions that we considered in Section 2 related the reactant concentrations to the reaction rate. In many cases, however, the quantity of a reactant remaining after a given amount of time has passed is of more interest than the speed at which the reaction is occurring. In the mathematics of calculus, the rate law expressions are differential equations. If these are integrated, we obtain equations for the concentration as a function of time. Since calculus is not a prerequisite for General Chemistry II, only the final equations will be presented. The calculus need to get them will be skipped.
For simplicity, we will only consider reactions in which there is a single reactant. That is, reactions of the form
aA ----------> products
where a is a stoichiometric coefficient and A is a chemical formula. Such a reaction would have a rate law in terms of that single reactant A. We would expect the rate law to have the form
Rate = k [A]x
where x will equal 0, 1, or 2, because we are only going to consider zero, first, and second order reactions. The equation we obtain for the time dependence of concentration depends on the order of the reaction. The equations are often presented in a form that makes it obvious that a linear plot can be constructed. These plots are useful to test whether or not a reaction is of a particular order, and also allow us to determine the reaction rate constant. Here are the integrated rate laws for reactions of zero, first, and second order in a single reactant:
Zero Order: [A]t = [A]0 - kt
First Order: ln [A]t = ln [A]0 - kt
1
1
Second Order: ------- =
------- + kt
[A]t
[A]0
In the above equations, [A]0 is the initial concentration of substance A (the concentration at the start of the reaction or "time zero"), [A]t is the concentration of substance A after a period of time t has elapsed, and k is the rate constant. If we compare the above three integrated rate laws to the equation for a straight line,
Y = m . X + b
we see that each of them suggests a linear plot as follows:
Zero Order: If the reaction is zero order, a plot of [A]t on the Y-axis against t on the X-axis gives a straight line that has a slope of -k and a Y-axis intercept of [A]0.
First Order: If the reaction is first order, a plot of ln [A]t on the Y-axis against t on the X-axis gives a straight line that has a slope of -k and a Y-axis intercept of ln [A]0.
Second Order: If the reaction is second order, a plot of 1 / [A]t on the Y-axis against t on the X-axis gives a straight line with a slope of k and a Y-axis intercept.
We have seen in Section 2 how initial rate studies (multiple experiments with different initial reactant concentrations) can be used to determine the rate law of a chemical reaction. But if the reaction involves only a single reactant, that is, one of the form
aA ----------> products
the integrated rate laws presented above allow a means of determining the rate law in a single experiment. A convenient starting concentration of substance A is used, and the concentration of substance A is measured at regular time intervals. The concentration is then plotted against time as a linear plot ([A]t vs. t), a logarithmic plot (ln [A]t vs. t), and a reciprocal plot (1 / [A]t vs. t). The plot that comes closest to a straight line indicates the order of the reaction. If it is the linear plot, the reaction is zero order; if it is the logarithmic plot, the reaction is first order; and if it is the reciprocal plot, the reaction is second order. In all cases, the slope of the line is used to get the rate constant. For the zero and first order plots, the line will have a negative slope. We simply ignore the negative sign. The rate constant is the magnitude of the slope, taken as a positive number. For the second order plot, the line has a positive slope, and the slope is equivalent to the rate constant, with no modification being required.
In addition to their utility in constructing graphical plots, the integrated rate laws are also useful for algebraic calculations. The following examples illustrate their use:
Example 1:
The decomposition of hydrogen iodide is described by the following equations:
2HI(g) ----------> H2(g) + I2(g)
Rate = k [HI]2
At 427 oC, the rate constant k has the value 1.20 x 10-3 mol-1 L s-1. If the initial concentration of HI is 0.560 mol L-1, what will the HI concentration be after 2.00 hours of reaction time?
Solution:
Since the rate constant has the time units in seconds, we must convert the 2.00 hour of reaction time to seconds:
60
min
60 s
2.00 h x ---------
x -------- = 7200 s
1
h
1 min
The other quantities we need are [HI]0 = 0.560 mol L-1 and k = 1.20 x 10-3 mol-1 L s-1. From these, we can calculate [HI]t. The rate law indicates that this is a second order reaction, so we use the second order integrated rate law. Substituting HI for the generic substance A in that equation, we have
1
1
------- = -------
+ kt
[HI]t
[HI]0
Substituting our numerical values into this equation, we have
1
1
------- =
------------------ + 1.20 x 10-3 mol-1
L s-1 (7200 s)
[HI]t
0.560 mol L-1
1
------- = 1.7857 mol-1
L + 8.64 mol-1 L
[HI]t
1
------- = 10.4257 mol-1
L
[HI]t
The above is still the reciprocal concentration, however. We must take the reciprocal of both sides of this equation to get the actual concentration. The reciprocal of 1 / [HI]t is [HI]t. To get the reciprocal of the number on the right hand side, we enter the number in our calculator and press the key that says 1/x or x-1. If the answer is not immediately displayed, the = or EXE key needs to be pressed. To get the reciprocal of the units, change the sign of the exponents. The reciprocal of mol-1 L is mol L-1.
[HI]t = 0.09592 mol L-1
Example 2:
The decomposition of sulfuryl chloride, SO2Cl2 is described by the following equations:
SO2Cl2(g) ----------> SO2(g) + Cl2(g)
Rate = k [SO2Cl2]
At 320 oC, the rate constant k has the value 2.20 x 10-5 s-1. If the reaction begins with SO2Cl2 at an initial concentration of 1.00 x 10-4 mol L-1, how long will it take for the SO2Cl2 concentration to be be reduced to 2.50 x 10-5 mol L-1?
Solution:
The rate law indicates that this is a first order reaction, so we use the first order integrated rate law. Substituting the generic substance A in the equation with SO2Cl2, we have
ln [SO2Cl2]t = ln [SO2Cl2]0 - kt
Since we are asked how long something will take, we need to solve the equation for time. To do this, begin by transposing the initial concentration of SO2Cl2 to the left hand side.
ln [SO2Cl2]t - ln [SO2Cl2]0 = -kt
Multiplying the equation by -1, and changing the order of addition on the left so that the positive term appears first, we have
ln [SO2Cl2]0 - ln [SO2Cl2]t = kt
The difference of two logs is equal to the log of the quotient, so the equation can now be written
| --
[SO2Cl2]0
--|
ln |
----------------- |
= kt
|--
[SO2Cl2]t
--|
The last step is to multiply by 1 / k on both sides. This isolates t.
1 |--
[SO2Cl2]0 --|
t = ------ ln |
-------------- |
k |--
[SO2Cl2]t --|
In this problem, we have [SO2Cl2]0 = 1.00 x 10-4 mol L-1, [SO2Cl2]t = 2.50 x 10-5 and k = 2.20 x 10-5 s-1.
1
|-- 1.00 x 10-4 mol L-1
--|
t = ----------------- ln
| ----------------------- |
2.20 x 10-5
s-1 |--
2.50 x 10-5 mol L-1 --|
t = 45455 s ln (4.00) = 45455 s (1.3863) = 6.30 x 104 s
If the time is desired in minutes or hours, a unit conversion must be done.
1 min
6.30 x 104 s x -----------
= 1.05 x 103 min
60 s
1
h
1.05 x 103 min x ----------
= 17.5 h
60 min
One way to gauge the speed of a reaction is to specify the amount of time required for a reactant concentration to be reduced to half its original value. The faster the reaction, the less time required for the concentration to be cut in half. We use the symbol t½ to refer to the half life. The ½ serves as a label here. We should not interpret it as being multiplied by the time t. Since the concentration at the half life time (t½) is half the starting concentration, we can represent it as ½[A]0. In Section 3.1, we consider reactions of the form
aA ----------> products
which were either zero, first, or second order. If we take the integrated rate laws for each of these reactions (as presented in Section 3.1) and make the substitutions t = t½ and [A]t = ½[A]0 we obtain the equations for half life for each of these reaction orders.
For the zero order, we start with
[A]t = [A]0 - kt
and substitute t = t½ and [A]t = ½[A]0 to get
½[A]0 = [A]0 - kt½
By transposing the [A]0 from the right side to the left side (subtracting [A]0 from both sides) we get
½[A]0 - [A]0 = -kt½
The subtraction on the left gives -½[A]0 so we now have
-½[A]0 = -kt½
Dividing both sides of this equation by -k gives
½[A]0
[A]0
t½ = ---------- =
---------
k
2k
The above is our final equation for the half life of a zero order reaction. Two forms have been presented because the the ½ in the numerator can be re-expressed as a 2 in the denominator. The student can use whichever form (s)he prefers.
Before going on to consider the first order reaction, let's look at the features of the zero order half life equation we just derived. Since the initial reactant concentration ([A]0) is in the numerator, the half life will increase with the initial concentration. The greater the concentration of the reactant, the longer it will take for half of it to be consumed. We can explain this feature as follows:
The rate law for a reaction that has a single reactant (referred to generically as A) and is zero order in that reactant is
Rate = k [A]0 = k (1) = k
Since any quantity raised to the zero power is equal to 1, the concentration factor simply drops out of the equation and is replaced by 1. Then, since any quantity multiplied by 1 is equal to itself, the reaction rate is equal to the rate constant. That is,
Rate = k
The rate of a zero order reaction does not depend on the reactant concentration! At first glance, this seems strange, considering that it was pointed out in Section 1 that molecules must collide in order to react. A reaction is zero order when a factor other than collision frequency and collision energy (activation energy) controls the rate. For example, if a reaction must absorb light in order to occur, the availability of photons of the proper energy might be what limits the rate of the reaction. Increasing the concentration does not increase the rate in this case. You will have a greater concentration of reactant molecules, but they all must "wait" for an incoming photon to energize them.
Since the rate of a zero order reaction does not depend on the reactant concentration, it will continue at a constant rate as the reactant is consumed. This is in contrast to reactions of other orders, for which the rate decreases as the reactant is consumed, due to the decreasing collision frequency. If the reaction proceeds at a constant rate, then of course, the greater the amount of reactant you have, the longer it will take to use it up. This same argument applies if we consider the time required to use up half of it. Therefore, half life should increase with the initial concentration of the reactant. This is exactly what our half life equation shows us.
The half life equation also shows that the half life decreases with the rate constant. The rate constant is in the denominator, so the larger it is, the smaller (i.e., shorter) the half life will be. This is logical. A larger rate constant means a faster reaction. The faster the reaction, the more quickly the reactant is used up, and therefore, the more quickly half of it is used up.
Now lets consider the first order reaction. We start with the integrated rate law
ln [A]t = ln [A]0 - kt
and substitute t = t½ and [A]t = ½[A]0 to get
ln (½[A]0) = ln [A]0 - kt½
On the left hand side, we can use the fact that the log of a product is the sum of the logs. This allows us to split up the ½ and the [A]0 and write
ln ½ + ln [A]0 = ln [A]0 - kt½
Since ln [A]0 appears on both sides, it can be canceled out (mathematically what we do is subtract it form both sides). This leaves
ln ½ = -kt½
Another way to think of ½ is 2-1. Our equation can now be written
ln 2-1 = -kt½
Since the log of a number raised to a power is equal to the power multiplied by the log of the number, we can take the power of -1 on 2 and place it in front of the ln. This merely puts a negative sign in front of it. We now have
-ln 2 = -kt½
The negative sign appears on both sides and can be canceled. Mathematically, what we are doing is multiplying both sides by -1. We now have
ln 2 = kt½
Now, dividing both sides by k, and reversing the order in which we write the equation, so that t½ appears on the left side, we have
ln 2
t½ = -----
k
This is our final result for the half life of a first order reaction. It is an interesting result in that the initial reactant concentration, [A]0 does not appear. This means that the half life of a first order reaction is independent of the starting concentration. No matter how much or how little you have, it still takes the same amount of time to get rid of half of it. How can this be? To understand this phenomenon, let us look at the rate law for a reaction that is first order in a single reactant.
Rate = k [A]1 = k [A]
Since any quantity raised to the first power is equal to itself, the rate is equal to the product of the rate constant and the reactant concentration. If you double the reactant concentration, you will double the rate. This is why the half life is independent of initial concentration. If you increase the reactant concentration -- which might seem like it should make it take longer to use it up -- you also increase the rate by the same factor. As a result, you always break even, no matter how much you increase the concentration.
The rate constant again appears in the denominator, just as it did in the zero order reaction. Therefore, once again, a higher rate constant will give a shorter half life. The explanation here is the same as before. A higher rate constant means a faster reaction, and if the reaction is faster, it should not take as long to consume half of the reactant.
Now let's consider the reaction that is second order in a single reactant. We take the integrated rate law
1
1
------- =
------- + kt
[A]t
[A]0
and substitute t = t½ and [A]t = ½[A]0 to get
1
1
-------- = --------- + kt½
½[A]0
[A]0
On the left hand side, we see a fraction within a fraction. If we multiply the numerator and denominator of the "big" fraction by 2, we can clear the "little" fraction in the denominator, because 2 times ½ is 1. This does not change the value of the "big" fraction because in multiplying the numerator and denominator by the same number (both get multiplied by 2), we have multiplied the "big" fraction by 1. Our equation now looks like this:
2
1
-------- = --------- + kt½
[A]0
[A]0
If we subtract 1 / [A]0 from both sides, we have
2
1
------- - ------
= kt½
[A]0
[A]0
On the left side, the two fractions have a common denominator ([A]0) so we can simply subtract the numerators. We now have
1
------- = kt½
[A]0
Dividing both sides by k (or multiplying by 1/k if you prefer to think of it that way) and reversing the order of writing the equation so that t½ appears on the left, we now have
1
t½ = -------
k[A]0
This is the our final result for the half life of a second order reaction. Notice that the initial concentration of the reactant ([A]0) now appears in the denominator. This means that the greater the reactant concentration is, the shorter the half life will be! How can this be? You have more of it, and it takes less time to get rid of half of it than if you had less of it. As we have seen with the reaction orders we considered earlier, we look to the rate law to understand the characteristics of the half life. For a reaction that is second order in a single reactant, the rate law is
Rate = k [A]2
Since the rate depends on the square of the concentration rather than the concentration itself, if we double the concentration, the rate is increased by a factor of 4. This is because the factor of 2 increase in concentration gets squared to produce a factor of 4 increase in the rate. So the reaction rate increases faster than the concentration. That is why larger concentrations have shorter half lives than smaller concentrations.
As usual, the rate constant is in the denominator, meaning that the larger the rate constant is, the shorter the half life will be. As we have seen, this is because a larger rate constant means a faster reaction, and the faster the reaction, and less time it should take to consume half of the reactant.
In summary then, we find the following features pertaining to half lives:
On your general chemistry exams, you may encounter questions about half lives. But you will also find that sometimes half life calculations can be used as a shortcut for other problems that don't ask for the half life per se. To illustrate this, let's re-work one of the problems posed in Section 3.1, using a half life approach. The problem, which you have seen earlier, is the following:
The decomposition of sulfuryl chloride, SO2Cl2 is described by the following equations:
SO2Cl2(g) ----------> SO2(g) + Cl2(g)
Rate = k [SO2Cl2]
At 320 oC, the rate constant k has the value 2.20 x 10-5 s-1. If the reaction begins with SO2Cl2 at an initial concentration of 1.00 x 10-4 mol L-1, how long will it take for the SO2Cl2 concentration to be be reduced to 2.50 x 10-5 mol L-1?
Solution via a Half Life Approach:
Notice that the ending concentration is ¼ of the initial concentration:
1.00 x 10-4 mol L-1
-------------------- = 2.50 x 10-5 mol L-1
4
To reduce a reactant to ¼ of its original concentration should require 2 half lives. This is because in the first half life, the reactant concentration will be reduced to half of its original value, and in the second half life, that "new" concentration (half of the original) will again be cut in half so it now amounts to only ¼ of the original value. Since the half life of a first order reaction does not depend on concentration, the second half life will be the same duration as the first. In fact, every half life in a first order reaction will be the same duration as the first. So if we need an integer number of half lives (i.e., 2 half lives, 3 half lies, 4 half lives, etc), we can calculate the half life just once and then multiply by the number of half lives we need. In this case, we need 2 half lives so we calculate the first order half life and multiply that result by 2.
ln
2
ln 2
t½ = ----- =
---------------- = 31507 s
k 2.20 x 10-5
s-1
Every 31507 seconds, the concentration is reduced to half of what it was at the beginning of that time interval. So if we start with a concentration of 1.00 x 10-4 mol L-1, we will find that 31507 seconds later, the concentration will be only 5.00 x 10-5 mol L-1. That is,
1.00 x 10-4 mol L-1
-------------------- = 5.00 x 10-5 mol
L-1
2
If we now take the 5.00 x 10-5 mol L-1 as the "new" starting concentration and wait another 31507 seconds, that concentration will also be cut in half:
5.00 x 10-5 mol L-1
-------------------- = 2.50 x 10-5 mol L-1
2
We had to wait for 2 half lives and they were each 31507 seconds in duration. Our total waiting time has been
2 (31507 s) = 63014 s » 6.30 x 104 s
The above is our answer to the problem. If we prefer the answer in minutes or hours, we can convert the units.
1 min
63014 s x
------- = 1050 min
60 s
1 h
1050 min x
-------- = 17.5 h
60 min
These are the same answers we got in Section 3.1, but the work required in this section was much shorter.
The shortcut we took advantage of here does not always work. So let's discuss when it will work. First, we must be seeking a "good" fraction of the original concentration. The fraction ¼ is one of those "good" fractions. A "good" fraction is one that is obtained after an integer number of half lives. As we have seen, we have ½ the original concentration in 1 half life, and ¼ the original concentration in 2 half lives. If we continue taking half of what we had before, we find that ½ of ¼ is 1/8, ½ of 1/8 is 1/16, ½ of 1/16 is 1/32, and so on. In general, the fraction remaining after n half lives is 1/2n where n is a positive integer (whole number). So if we wanted to know how long it would take for the concentration to be reduced to 1/3 of its original value, we would have to solve the problem using the longer method illustrated in Section 3.1. The fraction 1/3 is not a "good" fraction -- that is, it does not correspond to an integer number of half lives.
Also, the shortcut is most convenient for first order reactions, because their half life does not change as the reactant gets used up in the reaction. While we could, in principle, apply the shortcut to reactions of zero or second order, it would not be as much of a shortcut. We could not just calculate the half life once and then multiply by the number of half lives we need, because the half life would keep changing. We would need to determine the time interval required for each half life and then add all of these times together. To illustrate the difference in half life characteristics for reactions of zero, first, and second order, consider these three reaction orders all starting out with a half life of 32 minutes. We can construct the following table showing number of elapsed half lives, fraction of reactant remaining, and total reaction time.
|
# of Half Lives |
Fraction Remaining |
Zero Order |
First Order |
Second Order |
|
0 |
1 |
0 min |
0 min |
0 min |
|
1 |
½ |
32 min |
32 min |
32 min |
|
2 |
¼ |
48 min |
64 min |
96 min |
|
3 |
1/8 |
56 min |
96 min |
224 min |
|
4 |
1/16 |
60 min |
128 min |
480 min |
|
5 |
1/32 |
62 min |
160 min |
992 min |
Notice that the fraction of reactant remaining after any number of half lives is the same for all reaction orders. However, the total reaction times are quite different when we compare the different reaction orders.
The first order is the easiest to understand, in terms of half lives. In the table above, all the half lives for this order are 32 minutes long. This is because the half life is independent of concentration, so if the first half life is 32 minutes, they all will be. Looking down the column for First Order Reaction Time, notice that each time is 32 minutes more than the one before it. If you multiply the number of half lives by 32 minutes, you get the total reaction time in the first order reaction.
For the zero order reaction, the half life decreases with the concentration. When the concentration is only half what it used to be, the half life will only be half as long. So if the first half life is 32 minutes, the second half life will be only 16 minutes. The total reaction time over the first 2 half lives will be 48 minutes (32 minutes plus 16 minutes). The third half life will be only half as long as the second half life (16 minutes) meaning it will be only 8 minutes long. The total reaction time over the first 3 half lives will be 56 minutes (32 minutes plus 16 minutes plus 8 minutes). The fourth half life will be only half as long as the third (8 minutes) meaning it will be only 4 minutes long. The total reaction time over the first 4 half lives will be 60 minutes (32 minutes plus 16 minutes plus 8 minutes plus 4 minutes). The fifth half life will be only half as long as the fourth (4 minutes) meaning it will be only 2 minutes long. The total reaction time over the first 5 half lives will be 62 minutes (32 minutes plus 16 minutes plus 8 minutes plus 4 minutes plus 2 minutes).
For the second order reaction, the half life increases as the concentration decreases. When the concentration is only half what it used to be, the half life will be twice as long. So if the first half life is 32 minutes, the second half life will be 64 minutes. The total reaction time over the first 2 half lives will be 96 minutes (32 minutes plus 64 minutes). The third half life will be twice as long as the second half life (64 minutes) meaning it will be 128 minutes long. The total reaction time over the first 3 half lives will be 224 minutes (32 minutes plus 64 minutes plus 128 minutes). The fourth half life will be twice as long as the third (128 minutes) meaning it will be 256 minutes long. The total reaction time over the first 4 half lives will be 480 minutes (32 minutes plus 64 minutes plus 128 minutes plus 256 minutes). The fifth half life will be twice as long as the fourth (256 minutes) meaning it will be 512 minutes long. The total reaction time over the first 5 half lives will be 992 minutes (32 minutes plus 64 minutes plus 128 minutes plus 256 minutes plus 512 minutes).
We noted in Section 1.1.5 that the temperature affects a reaction's rate -- the higher the temperature, the faster the reaction rate. In this section, we consider the manner in which the reaction rate increases with temperature. The temperature dependence of reaction rate is found in the rate constant. To see this, consider the generic reaction and rate constant
aA + bB ----------> cC + dD
Rate = k [A]x [B]y
This reaction will have a higher rate at a higher temperature, even if we use the same reactant concentrations as we did at the lower temperature. Assuming the reaction orders (x and y) are the same at the higher temperature (and they should be unless the reaction somehow follows different kinetics at the higher temperature), the only way we can get a higher Rate is if the value of k is larger. Therefore, the rate constant k must be temperature dependent. The manner in which the rate constant depends on temperature is given by the Arrhenius equation:
|-- Ea
--|
k = A . exp |
- --------- |
|-- RT
--|
In the above equation, A is a pre-exponential factor, not to be confused with [A] with brackets around it, which refers to the concentration of "substance A". The A in the above equation is called the frequency factor, because it accounts for the collision frequency of the reactant molecules. The exp part of the equation is the energy factor, and accounts for the fraction of reactant molecules that will have enough energy to react. The variable Ea is the activation energy, R is the gas constant (which has the value 8.314510 J / mol K) and T is temperature, which MUST be expressed in Kelvin units. The function exp is the inverse of the natural logarithm ln. That is, exp(x) is another way of writing ex. It is useful when the argument of the inverse natural logarithm is a complicated function, because you can avoid having to write that function as a superscript. The pre-exponential factor or "frequency factor" is slightly temperature dependent, because at higher temperatures the molecules are moving faster and collide more often. However, we saw in Section 1.1.5 that changes in collision frequency contribute only about 3% of the change in reaction rate. By far, the inverse natural logarithm term is the major contributor to the change in reaction rate as temperature is changed. Therefore, we will simplify matters and derive an approximate equation by treating A as a constant, ignoring its slight temperature dependence.
We can re-write the Arrhenius equation presented above in a form that suggests a linear plot. From this plot, we can determine the activation energy of the reaction. We begin by taking the natural logarithm of both sides of the equation. We then have
|--
|-- Ea
--| --|
ln k = ln | A .
exp | - ----------
| |
|--
|-- RT
--| --|
Since the log of a product is equal to the sum of the logs, we can split the frequency factor and the energy factor on the right hand side.
|-- |--
Ea --|
--|
ln k = ln
A + ln |
exp | - ----------
| |
|-- |--
RT --| --|
In the second term on the right hand side, the ln and exp cancel each other out because they are inverse functions. This leaves the following expression:
Ea
ln k = ln A
- ----------
RT
Now factor the fraction Ea/RT into two fractions as follows:
|-- Ea
--| |--
1 --|
ln k = ln A
- | -----------| . |
------ |
|-- R --|
|-- T --|
Comparing the above equation to the equation for a straight line,
Y = m .X + b
we see that ln k plays the role of Y, 1/T plays the role of X, -Ea/R plays the role of m, and ln A plays the role of b. In Sections 2.3 and 3.1, we saw experimental methods by which the rate law of a chemical reaction could be determined. The rate constant that is determined in those experiments only applies to the temperature at which the experiment is conducted, because rate constants are temperature dependent. If the experiments are repeated at several different temperatures, we can compile a list of temperatures and corresponding rate constants at those temperatures. We then take the natural logarithm of all the rate constants and the reciprocal of all the temperatures (which must be expressed in Kelvin units). If we them plot ln k on the Y-axis against 1/T on the X-axis, hopefully the points will approximately fall on a straight line. The slope of this line is -Ea/R. Since R is a known constant, the activation energy Ea can be calculated if the slope is measured.
Ea = -R . Slope where R = 8.314510 J / mol K
Activation energies are never negative. The line on this plot will have a negative slope, and this will cancel the negative sign in front of R, leaving a positive value for the activation energy.
The graphical method described above for determining activation energies is most useful when the rate constant has been measured at several different temperatures. If the rate constant has only been determined at two different temperatures, we might as well just calculate the activation energy algebraically. Certainly, any two points will determine a straight line. One of the principal benefits of constructing a graphical plot is that a "bad" experiment (that is, one in which errors have been made) stands out as a data point that falls out of line with the other points on the plot. The erroneous experiment can then be excluded from the calculations. Activation energies obtained from the slope of the line tend to be more reliable than those calculated algebraically from a pair of measured temperatures and rate constants. We can think of the activation energy calculated from the slope of the line as a kind of "average" based on all the data used to plot the line. Using a larger set of data to determine an average tends to give a "better" (i.e., more accurate) average. As a student, you might appreciate this analogy: If you make a "B" on your very first quiz in chemistry (near the beginning of the semester), it's too early to say what kind of student you are. You might be an "A student" who just had a bad day. Or perhaps you are a "C student" who just got lucky. But if you still have a "B" average near the end of the semester after having taken 4 exams and 15 quizzes, it is a safe bet that you are a "B student". Nevertheless, it is still common practice in general chemistry to include questions on exams in which students are to calculate activation energies, rate constants, or temperatures based on only a pair of measured data. Such calculations are less time consuming than constructing graphical plots, and therefore, better suited to timed exams. For this reason, we need to derive a "two point" form of the Arrhenius equation that can be used to solve common general chemistry problems involving rate constants, activation energies and temperatures.
We can derive the needed equation starting from the equation for the linear plot. We write this equation twice, replacing the generic k and T with k1 and T1 in one of the equations and with k2 and T2 in the other. In what follows, the equation with k2 and T2 is written first and the equation with k1 and T1 is subtracted from it.
|-- Ea
--| |--
1 --|
ln k2 = ln A
- | -----------| . |
------ |
|-- R --|
|-- T2 --|
|-- Ea
--| |--
1 --|
ln k1 = ln A
- | -----------| . |
------ |
|-- R --|
|-- T1 --|
In subtracting the equation with the variables labeled with a number 1 from the equation with the variables labeled with a number 2, note the following:
At this point, we can write
|-- Ea
--|
|
1
|
|-- Ea
--|
|-- 1 --|
ln k2 - ln k1 =
| ---------- | . |
--------- | - | ---------
| . | ------- |
|--
R --|
| T1
--|
|-- R --|
|-- T2 --|
On the left side of the above equation, the difference of two logarithms can be expressed as the logarithm of the quotient. On the right hand side, we can factor out the quantity (Ea / R) that is common to both terms. With these adjustments, our equation now looks like this
|-- k2
--| |--
Ea --|
|--
1
1 --|
ln | ------- | =
| ------- | . |
------- - ------- |
| k1
--| |--
R --| |--
T1
T2 --|
This is the form in which the equation is usually presented, and the form in which you should memorize it. Although there are 5 parameters in this equation (k2, k1, Ea, T1, and T2), there are only 3 types of problems you will work with this equation. You can solve for an unknown rate constant, an unknown activation energy, or an unknown temperature. It does not matter which rate constant and temperature pair you assign to k1 and T1 and which you assign to k2 and T2, just as long as you don't criss-cross rate constants and temperatures. However, to reduce the chances of making an algebraic error, I recommend you solve for k2 instead of k1 (because it is easier to solve for things in the numerator) and that you solve for 1/T1 instead of 1/T2 (because 1/T1 does not have a negative sign in front of it). Notice that I said solve for 1/T1, not solve for T1. That is another recommendation. The equation looks rather awkward if you try to solve it for the actual temperature. If you can calculate the reciprocal temperature (1/T), you can always press the reciprocal key (labeled 1/x or x-1) to obtain the temperature itself. You must also remember that this is going to be the Kelvin temperature, so if you are wanting the temperature in Celsius units, you will need to subtract 273.15 from it. Presented below are the results of solving the above "two-point" Arrhenius equation for k2, Ea, and 1/T1. Only the final result is shown, not the algebra needed to get there. Students who want to see how the following forms are obtained should consult their instructor.
Solution for an unknown rate constant:
|-- Ea
|--
1
1 --| --|
k2 = k1 . exp
| ------- .
| ------- -
------- | |
|--
R |--
T1
T2 --| --|
Solution for an unknown activation energy:
|-- k2 --|
R .
ln | ----- |
|-- k1 --|
Ea = ----------------------
|--
1
1 --|
| ----- - ----- |
|--
T1 T2
--|
Solution for an unknown temperature:
1
1
R |-- k2
--|
----- = ----- + ----- .
ln | ----- |
T1
T2 Ea
|-- k1 --|
In Section 2.3, when the concept of the rate law and reaction orders was developed, we noted that reactions can be either elementary (occur in one step) or non-elementary. In that section, we noted that for elementary reactions, the reaction orders had to match the coefficients in the balanced equation, but for non-elementary reactions, there was no necessary relationship. In this section, we look at these facts in more detail.
As an example, consider the reaction
2NO2(g) + F2(g) ----------> 2NO2F(g)
If this reaction is elementary, its rate law would have to be
Rate = k [NO2]2 [F2]
because of the requirement that reaction orders and coefficients match. However, experimental data indicate that the rate law of this reaction is
Rate = k [NO2] [F2]
That is, the reaction is first order in NO2, even though the coefficient of NO2 is 2 in the balanced equation. This mismatch between a reaction order and a stoichiometric coefficient means that the reaction is definitely NOT elementary. If it is not elementary, then it must be the net effect of two or more other reactions that are elementary. With some chemical intuition, we can propose a reasonable set of chemical reactions (assumed to be elementary) by which the overall reaction might occur. Such a set of elementary reactions is called a reaction mechanism. To be accepted as a possibility, any reaction mechanism we propose must pass two tests:
If a proposed mechanism passes both of the above tests, it may be the correct mechanism -- but then again, it may not be. We can never prove with absolute certainty that we have the right mechanism, though in some cases we can show that a proposed mechanism can NOT be correct, and therefore, can be ruled out. This is the scientific method in action. Recall that you learned in General Chemistry I that a no hypothesis or theory can ever be proved with absolute certainty, though in some cases, they can be disproved.
For the reaction
2NO2(g) + F2(g) ----------> 2NO2F(g)
chemists have proposed the following 2-step mechanism
slow
Step 1: NO2(g)
+ F2(g) ----------> NO2F(g)
+ F(g)
fast
Step 2: NO2(g)
+ F(g) ----------> NO2F(g)
----------------------------------------------------------------------
Total: 2NO2(g)
+ F2(g) ----------> 2NO2F(g)
In the above mechanism, the monatomic fluorine, F(g) cancels out because it is both a reactant (Step 2) and a product (Step 1). Chemical species like these, that arise naturally in the course of a reaction sequence, but cancel out when the reactions are added, are called reaction intermediates. Thus, the F(g) is a reaction intermediate in this mechanism. Often, there is a big difference in reaction rates for different steps in the mechanism. In this mechanism, Step 1 has been identified as slow and Step 2 as fast. We can justify this choice on the basis of the unstable and highly reactive nature of monatomic fluorine. Fluorine is one of seven elements that is found in nature in the diatomic state (that is, as F2). Fluorine is the most reactive of all the elements, especially when it is in monatomic form. Because fluorine is so highly reactive, we would expect to find it somewhat difficult to form it in the monatomic state, in which the F atom is not bonded to anything. Once formed, however, it would be reasonable to conclude that it will rapidly react with anything it encounters with which it is capable of reacting. It is on this basis that Step 1 has been labeled slow and Step 2 has been labeled fast.
To predict the rate law from a reaction mechanism, we need only look at the slowest step. The overall reaction, which depends on completing all the steps in the mechanism, can not be completed any faster than that slowest step can be completed. Therefore, the rate law for the slowest step will be the rate law for the overall reaction. We can write the rate law for the slowest step by inspection, because it, like all steps in the mechanism, is assumed to be elementary. In Step 1 of the proposed mechanism, the reactants are NO2 and F2. Each of these substances has a coefficient of 1, so Step 1 must be first order in each. That is, the rate law predicted by the mechanism is
Rate = k [NO2] [F2]
This is in agreement with experimental data. While this does not absolutely prove that the reaction occurs by this mechanism, it certainly seems plausible that it might occur this way, and it explains our experimental observations. This mechanism will likely continue to be accepted by chemists unless someone uncovers new data that suggests a different mechanism for the reaction.
Now let us consider another reaction:
2NO(g) + Cl2(g) ----------> 2NOCl(g)
The experimentally determined rate law for this reaction is
Rate = k [NO]2 [Cl2]
Comparing the reaction orders to the coefficients in the balanced equation, we see that everything matches. The coefficient of NO is 2, and the reaction is second order in NO, while the coefficient of Cl2 is 1 and the reaction is first order in Cl2. Looking only at the match between coefficients and exponents (reaction orders), it is possible that the reaction is elementary. However, we can argue on other grounds that it is not likely to be. If this reaction is elementary, it involves a 3-body collision. Two molecules of NO and one molecule of Cl2 -- a total of 3 molecules -- must all collide simultaneously. Three-body collisions are extremely rare, so if the reaction really did occur this way, it should be a very slow reaction. If the observed rate of the reaction is higher than what appears to be reasonable for a 3-body collision, then we must look for a mechanism to explain it, even though the match between coefficients and reaction orders "allows" for an elementary reaction. When we propose a mechanism, we generally try to avoid reactions that involve 3 or more particles coming together at the same time.
Let us try a strategy similar to what we used before:
slow
Step 1: NO(g) + Cl2(g)
----------> NOCl(g) + Cl(g)
fast
Step 2: NO(g) + Cl(g)
----------> NOCl(g)
------------------------------------------------------------
Total: 2NO(g) + Cl2(g)
----------> 2NOCl(g)
As shown above, this mechanism produces the overall reaction when the steps in the mechanism are added. So it has passed the first test. But it still has to predict the correct (i.e., experimentally determined) rate law in order to have any possibility of being correct. Step 1 has been labeled slow and Step 2 as fast on the same grounds as discussed previously: Step 1 produces the highly reactive Cl intermediate, while in Step 2, this very reactive species reacts with NO to make a stable molecule. If we base the rate law on the slow step (Step 1), we obtain
Rate = k [NO] [Cl2]
But this is not in agreement with the experimentally determined rate law, which is
Rate = k [NO]2 [Cl2]
Because the rate law predicted by the mechanism does not conform to experimental observations, this mechanism must be rejected as incorrect. We are then still left with the question of how this reaction occurs. Unless the reaction is very slow, "giving up" and saying the reaction is elementary is not a viable option. We still need a reaction mechanism that proposes nothing higher than 2-body collisions in any of its steps.
Having failed at our first attempt, now let's try the following mechanism:
fast, equil.
Step 1: NO(g) + Cl2(g)
<----------> NOCl2(g)
slow
Step 2: NO(g) + NOCl2(g)
----------> 2NOCl(g)
Mechanisms such as this, with an initial fast equilibrium step are quite common. By fast equilibrium, we mean that the first step rapidly reaches a state in which NO and Cl2 combine to form NOCl2 at the same rate that NOCl2 decomposes to form NO and Cl2. Using the slow step to predict the rate law gives us the result
Rate = k [NO] [NOCl2]
At first it may seem that we have failed again, since the experimentally determined rate law is
Rate = k [NO]2 [Cl2]
However, we are not finished yet. The predicted rate law can not be left in its present form, because it contains the quantity [NOCl2]. This is a reactive intermediate -- it does not appear in the overall reaction. The rate law for a chemical reaction should only include substances that appear in the overall reaction. Therefore, we must find a way to re-express the concentration of the intermediate NOCl2 in terms of the concentrations of substances that appear in the overall reaction. To do this, we will make use of the fact that Step 1 in the mechanism is at equilibrium. This means that the rate of the forward reaction in Step 1 is equal to the rate of the reverse reaction in Step 1. That is,
Rate1f = Rate1r
Remembering that the steps within a reaction are assumed to be elementary, we can write rate laws for them by inspection:
Rate1f = k1f [NO] [Cl2]
Rate1r = k1r [NOCl2]
Notice that for the reverse reaction, the right hand side of the equation is the reactant side. We normally think of things on the left side of a chemical equation as reactants and things on the right side as products. But reactants are what you start with and products are what you end up with. When you consider the reverse direction of a reaction, you start with the things on the right side and these become your reactants. Rate laws normally include the reactant concentrations, so our reverse rate law includes the quantity [NOCl2]. Since Rate1f and Rate2f are equal to each other, we can equate the right hand sides of the above two rate laws and write
k1f [NO] [Cl2] = k1r [NOCl2]
We only need to divide both sides of this equation by k1r to isolate [NOCl2] on one side of the equation. On the other side, the two constants can be written together in parentheses.
|-- k1f --|
[NOCl2] = | ----- |
[NO] [Cl2]
|-- k1r --|
This result can then be substituted into our predicted rate law:
Rate = k [NO] [NOCl2]
to obtain
|-- k1f --|
Rate = k [NO] | ----- | [NO] [Cl2]
|-- k1r --|
The above expression can be simplified. A collection of constants all multiplied and divided is just another constant. And the two factors of [NO] will multiply to produce [NO]2. Therefore, we can write the predicted rate law as
|-- k1f --|
Rate = k' [NO]2 [Cl2]
where k' = k
| ----- |
|-- k1r --|
We now see that the proposed mechanism predicts second order kinetics in NO and first order kinetics in Cl2, as required by the experimental data. Because the mechanism has been able to account for the observed kinetics, it can be accepted as a possibility. The agreement between the predicted and experimental rate laws does not prove that this is the correct mechanism, however.
Hopefully, having seen these examples, you can understand why the reaction orders may or may not match the coefficients in the balanced equation for a non-elementary reaction. The reaction for which you seek the rate law is just the overall process, but the rate is controlled by one of the elementary steps in the mechanism. If the rate determining step has coefficients for some of the reactants that differ from those that appear in the overall reaction, the reaction orders will not match the coefficients for those reactants. This was the case with the reaction
2NO2(g) + F2(g) ----------> 2NO2F(g)
Although the coefficient of NO2 was a 2, the reaction was first order in NO2 because the rate determining step was
NO2(g) + F2(g) ----------> NO2F(g) + F(g)
in which the coefficient of NO2 was a 1.
But even though the reaction orders don't have to match the coefficients in a non-elementary reaction, sometimes they do. This was the case with the reaction
2NO(g) + Cl2(g) ----------> 2NOCl(g)
The rate determining step in this reaction was
NO(g) + NOCl2(g) ----------> 2NOCl(g)
and when we express the concentration of NOCl2 in terms of NO and Cl2 (on the assumption that these three chemical species are in equilibrium), we obtain a rate law that happens to be second order in NO. Thus, the reaction order in NO has matched the coefficient in the balanced equation, but not because the reaction was elementary.
In Section 1.1.6, it was noted that a catalyst speeds up a chemical reaction without being consumed by the reaction. A catalyst works by lowering the activation energy for the reaction. Recall that the activation energy is the minimum energy that the colliding molecules must have in order to react. Even if the molecules collide in the correct orientation, they will simply bounce off of each other unchanged if the activation energy requirement is not met. At any given temperature, the higher the activation energy, the smaller the fraction of molecular collisions that will have enough energy to react. Conversely, the smaller the activation energy, the greater the fraction of molecular collisions that will have enough energy to react. Since a catalyst lowers activation energy, a chemical reaction will be faster with a catalyst than without one.
Earlier in these notes, we noted that I- serves as a catalyst in the decomposition of hydrogen peroxide, H2O2. Let us now look at the action of I- in more detail. The I- catalyzed decomposition of H2O2 is believed to proceed by the following mechanism:
slow
Step 1: H2O2(aq)
+ I-(aq) ----------> H2O(l)
+ IO-(aq)
fast
Step 2: H2O2(aq)
+ IO-(aq) ----------> H2O(l)
+ O2(g) + I-(aq)
-------------------------------------------------------------------------------------
Total 2H2O2(aq)
----------> 2H2O(l) + O2(g)
Notice that both the I- and the IO- cancel out when the reactions are added. The I- is a catalyst, because it has been physically added to the system. The IO- arises on its own and is therefore, a reaction intermediate. If the catalyst appears in the mechanism of the reaction it catalyzes (the usual case for homogeneous catalysts), it must always cancel out when the reactions are added to give the overall reaction. The catalyst can not be permanently used in the reaction, because then it would be a reactant. It may be temporarily "used", but it is always returned at the end of the reaction. The catalyst is recycled as the reaction occurs. In the above mechanism, the I- reacts with H2O2 to generate hypoiodite ions (IO-) which drives the O2 forming reaction in Step 2. In the process, iodide ions (I-) are re-generated, and can then be re-used in Step 1 to form more IO-. These processes are repeated over and over as the H2O2 decomposition occurs.
The I- catalyzed decomposition of H2O2 is faster than the uncatalyzed reaction because the rate determining step in the catalyzed mechanism (Step 1) has a lower activation energy than that of the uncatalyzed reaction. At room temperature, there will be a significant fraction of H2O2 molecules that lack sufficient energy to react via the uncatalyzed mechanism, but which have enough energy to enter the catalyzed reaction.