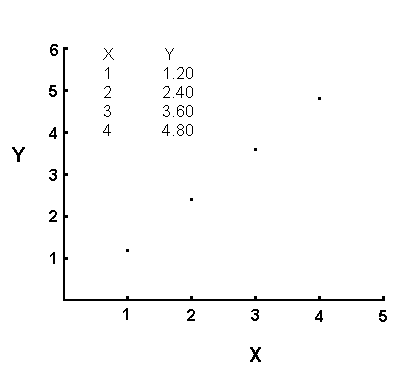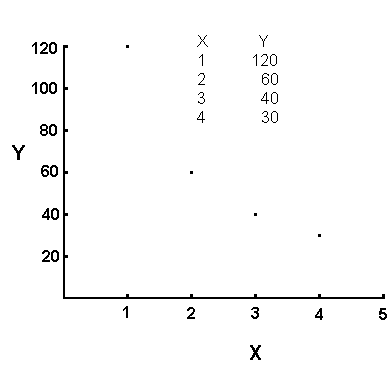THE GAS LAWS
1. Introduction
The gaseous state of matter is the easiest state to describe mathematically.
Under a wide range of conditions, gases of very different chemical composition
can be described by the same equations. Such an accomplishment is
not possible for liquids and solids. These states of matter vary
widely in their physical properties, and we can not use a "one size fits
all" approach to describe them. The physical properties of liquids
and solids are unique to the particular liquid or solid being considered.
The simplicity of gas phase properties arises mainly from the large
separation of the gas molecules from each other. In a solid or liquid,
the molecules are close together, so they can interact strongly with each
other. Physical properties of solids and liquids depend on how the
molecules interact with each other, which in turn, depend of their chemical
make-up. For this reason, each liquid or solid substance will have
its own unique properties. Because gas molecules are, on average,
quite well separated from one another, their interaction with each other
is very small. In many cases, we can treat the interaction as if
it were exactly zero. No real gas actually satisfies this
assumption, but most come close under a wide range of conditions.
A gas that actually has zero molecular interaction is purely hypothetical
and is called an ideal gas.
Most of the volume "occupied" by a gas is actually empty space -- the
space between the gas molecules. The volume occupied by the molecules
themselves is generally a very small fraction of the total gas volume.
For the hypothetical gas we call an ideal gas, the molecular volume
is considered to be exactly zero -- that is, the molecules of this
gas are considered to be point masses. They have mass but
occupy no volume.
At all temperatures above zero Kelvin, molecules are in motion.
The average kinetic energy of the molecules increases with temperature
-- that is, the higher the temperature, the faster the molecules are moving.
In a gas, each molecule moves in a straight line until it either collides
with another gas molecule or collides with the wall of its container.
In either case, it simply bounces off and continues in motion is a straight
line in another direction until the next collision. The pressure
exerted by a gas in a container is caused by the collission of the gas
molecules with the container walls.
The gas parameters we will be concerned with, and their algebraic symbols,
are as follows:
-
Pressure (P)
-
Volume(V)
-
Temperature (T)
-
Number of Moles (n)
We will develop the gas laws by considering how pressure and volume change
as each of the other of these quantities is changed. Before we do
that, however, we need to understand a couple of relationships that may
exist among paired data: the direct proportionality and the inverse proportionality.
2. The Direct Proportionality
If a set of paired data is related in such a way that the numerical values
of the X coordinate and the numerical values of the Y coordinate increase
(or decrease) together, and by the same factor, the data is said to show
a direct proportionality. Perhaps this can be made more clear by
use of an example. Consider the following set of data:
| X |
Y |
| 1 |
1.20 |
| 2 |
2.40 |
| 3 |
3.60 |
| 4 |
4.80 |
The data in this table shows a direct proportionality. If you
compare the X coordinate for the first two entries in the table, you find
X=1 for the first one and X=2 for the second one. The X increases
by a factor of 2 on going from the first entry to the second entry.
If you compare the Y coordinate for these same two entries, you discover
the same thing. Note that Y=1.20 for the first entry and Y=2.40 for
the second entry. On going from the first entry (row of the table)
to the second one, both the X and Y double.
An equation you can use to test a set of data to see if it is a direct
proportionality is the following:
X1
Y1
____
=
_____
X2
Y2
You test the data by designating one ordered pair as pair # 1 (having
coordinates X1 and Y1) and another ordered pair as
ordered paired # 2 (having coordinates X2 and Y2)
and substituting the corresponding values into the equation. If the
left and right sides are equal, you have a direct proportionality.
Another test for a direct proportionality is to graph the data. Data
which has a direct proportionality will plot as a straight line that passes
through the origin of the coordinate plane.
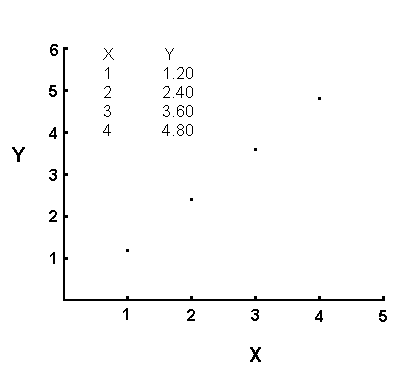
Mathematically, we say that Y is proportional to X and we write Y a
X.
We can make a proportionality into an equation by changing the proportionality
sign (a) to an equality sign (=) and multiplying
the right hand side by a constant, called a "constant of proportionality".
When this is done, we have Y = kX, where the symbol k has been used to
represent the constant. We can solve for the numerical value of the
constant k which characteizes the set of data by substituting any of the
ordered pairs from the set into the equation. Algebraically, we can
re-arrange the equation Y = kX to k = Y/X. Then if we substitute
the first of the ordered pairs into the equation, we have k = 1.20/1 =
1.20. Therefore, the complete equation is Y = 1.20X. We could
then use the equation to supply other ordered pairs that "belong" to this
set of data. For example, if X = 5 then Y = 1.20(5) = 6.00.
Thus, the ordered pair (5, 6.00) also belongs to this set of data, though
it was not originally included in the table of numbers used for the graph.
An "everyday life" example where you might encounter data that shows a
direct proportionality is buying something from a store. In this
case, let each item cost $1.20. Then X represents the number of such
items purchased and Y is the total purchase price. The physical meaning
of the constant in this example is the unit price.
3. The Inverse Proportionality
If a set of paired data is related in such a way that as one member of
the pair increases, the other member decreases, with the increases and
decreases being by the same factor, the data is said to show an inverse
proportionality. For example, consider the following set of data:
The data in this table shows an inverse proportionality. If you
compare the X coordinate for the first two entries in the table, you find
X=1 for the first one and X=2 for the second one. The X increases
by a factor of 2 on going from the first entry to the second entry.
If you compare the Y coordinate for these same two entries, you discover
that Y decreases by a factor of 2 on going from the first ordered
pair to the second one.
An equation you can use to test a set of data to see if it is a direct
proportionality is the following:
X1
Y2
____
=
_____
X2
Y1
You test the data by designating one ordered pair as pair # 1 (having
coordinates X1 and Y1) and another ordered pair as
ordered paired # 2 (having coordinates X2 and Y2)
and substituting the corresponding values into the equation. If the
left and right sides are equal, you have an inverse proportionality.
An inverse proportionality plots as a curve. The data in this
example yields the following graph:
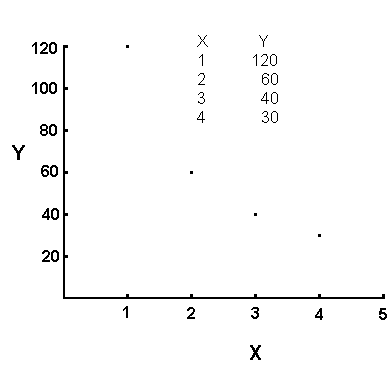
Graphing data is not the best way to determine if an inverse proportionality
exists, because there are many different shapes of curves in which data
can plot, and it is difficult to tell just by looking if your data has
the correct shape of curve to be considered an inverse proportionality.
The graphical test is more useful for a direct proportionality, because
it is easy to tell whether on not a set of points all fall on a straight
line. We must also remember that the straignt line defined by the
set of points must pass throught the origin of the graph (X = 0, Y = 0).
If not, the data merely increase (or decrease) together, but not by the
same factor. A true direct porportionality plots as a line passing
through the origin.
For inversely proportional data like that being considered here, we
can write Y a 1/X. As before, we can make
this an equation by changing the proportional sign (a)
to an equality sign(=) and multiplying on the right hand side by a constant.
This gives us Y = k/X. Rearranging this to k = XY and substituting
the values from the first ordered pair, we have k = (1)(120) = 120.
This is the value of the constant that is characteristic of this particular
set of data. We now have the complete equation for this set of data.
It is Y = 120/X. With this equation, we can find other ordered pairs
that belong to this set. For example, if X = 5, we have Y = 120/5
= 24. Thus, the ordered pair (5, 24) belongs to this set of data,
although it was not included in the table used to construct the graph.
4. The Empirical Gas Laws
Now that we understand the relationships known as the direct proportionality
(section 2) and the inverse proportionality (section 3) we are in a position
to "discover" the empirical gas laws.
4.1 Boyle's Law
Suppose we have a sample of a gas confined in a cylinder which has been
fitted with a movable piston. By moving the piston, we can adjust
the volume occupied by the gas. In addition, we can attach a pressure
meter and a temperature probe to the apparatus, allowing us to make simultaneous
measurements of pressure, temperature, and volume for the gas. Suppose
we had a sample of gas in the apparatus so that it occupied a volume of
2 liters and exerted a pressure of 3 atmospheres. (An atmosphere
is the "typical" pressure exerted by the earth's atmosphere at sea level.
It is the amount of pressure needed to support a column of mercury 760
mm high.) Now suppose we compress the gas (by pushing in the piston)
so that that same amount of gas must occupy a volume of only 1 liter.
Let us assume that the temperature does not change in this process.
Our objective here is to consider how the pressure changes as we change
the volume, while leaving the temperature and the number of moles of gas
constant. What pressure do you think the gas will exert after it
has been compressed to 1 liter?
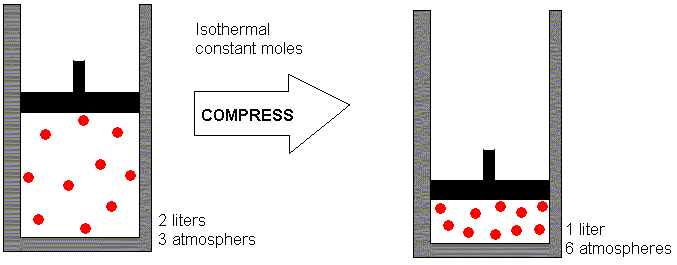
If you guessed 6 atmospheres, you got it right. When I give a
"chalk talk" on this topic, my students usually see the relationship --
I bet you did too. In predicting the new pressure, you have recognized
that that the relationship between pressure and volume (at constant temperature
and number of moles) is an inverse proportionality. The volume has
decreased by a factor of 2 (from 2 liters to 1 liter) so the pressure must
increase
by a factor of 2. This increases it from 3 atmospheres to 6 atmospheres.
Mathematically, then, we have that P a 1/V.
This is the most fundamental statement of Boyle's Law. In
words, Boyle's Law states that for a fixed amount (i.e. number
of moles) of gas, at constant temperature, the volume occupied by the gas
in inversely proportional to the applied pressure. We can make
an equation out of this in the manner described in section 3. Changing
the proportionality to an equality and multiplying by a constant, we have
P = k/V. This can be re-arranged to give PV = k. The constant
in this equation is not a true universal constant. In general, when
a proportionality (either direct or inverse -- this is true of both) is
made into an equation, the constant actually depends on those parameters
which affect the system but have been left out of the equation.
Clearly, the temperature affects the system, because if we were to heat
the 2 liter sample (arrangement on the left in the picture) without letting
it expand (for example, by holding the piston and not letting it move)
the pressure would increase. Also, if we were to pump additional
gas into the cylinder (through a gas inlet valve not shown in the picture)
the pressure would increase. Thus, the "constant" we have in the
equation PV = k actually changes as T and n change.
That is, k = f(T, n). This is the mathematical way of saying that
"k is a function of T and n". You may have seen this notation used
in one of your math classes. Have you ever seen someone write Y =
f(x)? Well, that is the sense in which I have written k = f(T, n).
The only difference is that it depends on 2 variables instead of only 1.
Since k depends on T and n, there is little point in trying to calculate
its value. We could, of course, obtain a value for the particular
arrangement shown in the picture by substituting values in the equation,
just as we did with our example data in section 3. However, this
value of the constant would not apply to a new sample with a different
number of moles of gas, or a sample at a different temperature. What
we will do instead is agree to only use this equation to deal with gas
calculations where both the temperature and the number of moles of gas
are not changing.
The gas will start out in a state of existence we will call "STATE 1".
Then, the gas will undergo a process that changes its pressure and volume,
but without changing its temperature or the number of moles of gas.
After the process is complete, the gas finds itself in a state of existence
we will call "STATE 2". Because we have not changed the temperature
or number of moles, we can apply Boyle's Law. When the gas is in
STATE 1, its pressure is symbolized by P1 and its volume by
V1. Similarly, in STATE 2, the pressure of the gas is
symbolized by P2 and the volume by V2. Now
apply Boyle's Law, in the form PV = k, to each state separately.
STATE 1: P1V1 = k
STATE 2: P2V2 = k
Now recall that k only depends on T and n, and neither of those has
changed in going from STATE 1 to STATE 2. Therefore, the value of
k must be the same in both states. This means that
P1V1 = P2V2
This is the 2-point form of Boyle's Law. It allows you to relate
the pressures and volumes of a gas in two states that are related through
some process in which the temperature does not change (i.e. isothermal)
and in which the number of moles do not change.
4.2 Charles' Law
In section 4.1, we left the temperature unchanged and saw how the pressure
and volume are related for a fixed amount (number of moles) of gas.
In this section, we change the temperature of a gas, and see how its volume
changes as we hold the pressure constant.
Suppose we have 2 liters of gas at a temperature of 300 Kelvin.
If we heat this gas (allowing it to expand during the heating process)
to 600 Kelvin, what do you suppose its volume will be?
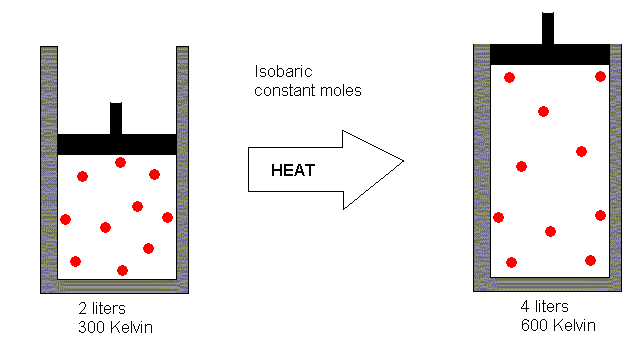
If you said 4 liters, you got it right. In making this estimate,
what you have done is recognized that the relationship between volume and
Kelvin is a direct proportionality. The Kelvin temperature was doubled
in the heating process, so you concluded the volume must have doubled also.
Mathematically, then, we have V a T.
This is the most fundamental statement of Charles' Law, which in
words, states that for a fixed amount (number of moles) of gas at constant
pressure, the volume is directly proportional to the Kelvin temperature.
As introduced in section 4.1, we can get an equation out of this by changing
the proportionality sign (a) to an equality
sign (=) and and multiplying on the right hand side by a constant.
This gives V = kT. As we have seen, the constant is often not a universal
constant, but is actually a function of those variables that are not represented
in the equation. In this case, the pressure (P) and the number of
moles (n) do not appear so k = f(P, n). Although we could find the
numerical value of the k for the apparatus shown above, there is little
point in doing so, since the k will be different each time we do the experiment
under a different pressure, or use a different number of moles of gas.
We will take an approach similar to that in section 4.1: we
will agree to only use the equation for those gas calculations in which
the pressure and number of moles are not changing.
Before the process (in the above example, heating) takes place, the
gas is in a state of existence we will call "STATE 1". In this state,
we refer to its volume as V1 and its Kelvin temperature as T1.
Then, after the process, the gas is in a state of existence we call "STATE
2". Here, we refer to the volume as V2 and Kelvin temperature
as T2. We can re-arrange the equation V = kT to get V/T
= k. Now we can apply this equation separately to STATE 1 and STATE
2.
STATE 1: V1 / T1 =
k
STATE 2: V2 / T2 =
k
Recall that k depends only on P and n. Since neither of these
variables changed on going from STATE 1 to STATE 2, the two k's are the
same. Therefore:
V1 / T1 = V2
/ T2
This is the 2-point form of Charles' Law. It is used to relate
the volumes and temperatures in two states that are connected by a process
in which the pressure does not change (i.e. isobaric) and in which the
number of moles does not change.
4.3 Gay-Lussac's Law (also called Amonton's Law)
In sections 4.1 and 4.2, the processes we carried out on a gas changed
its volume. We now consider a gas that has a fixed volume.
Experimentally, we can do this by having the gas confined in a rigid steel
tank, instead of a cylinder with a movable piston. The gas will always
occupy the full volume of the tank, and since the volume of the tank will
not change, the volume of the gas will be constant. In this experiment,
we will heat the gas and see how the pressure it exerts changes as the
Kelvin temperature changes.
If we start with a gas that is exerting a pressure of 1 atmosphere at
200 K, what pressure to you think it would exert if we heat it to 600 K?
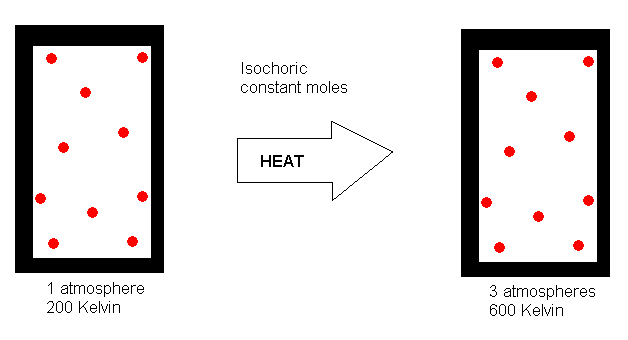
If you said 3 atmospheres, you got it right. What you have recognized
is that the pressure exerted by a fixed amout (number of moles) of gas
confined to a fixed volume is directly proportional to its Kelvin temperature.
Mathematically, we can write P a T.
As we have done twice before (sections 4.1 and 4.2) we wil make an equation
out of this by writing P = kT. Here, the "constant" will actually
depend on V and n since these do not appear in the equation. That
is, k = f(V, n). The numerical value of k will depend on the size
of tank we use, and on the amount (number of moles) of gas we put in it.
Therefore, there is no point trying to calculate its value. As usual,
we will simply agree to use this equation only for solving problems in
which the volume remains constant (i.e. isochoric) and in which the number
of moles of gas remains constant.
Before the process takes place (heating in this example, but it could
just as well have been cooling), the gas is in a state of existance we
will call "STATE 1". In this state, the pressure is symbolized by
P1 and the Kelvin temperature by T1. The process
carried out on the gas transforms its state of existence to that which
we call "STATE 2". Then the pressure is symbolized by P2
and the Kelvin temperatrue by T2. Now we take our equation,
P = kT, and re-arrange it to get P/T = k. We then apply this equation
separately to STATE 1 and STATE 2.
STATE 1: P1 / T1 =
k
STATE 2: P2 / T2 =
k
Recall that k only depends on the volume and number of moles of gas.
Neither of these has changed on going from STATE 1 to STATE 2, to the value
of k is the same in each state. This means that
P1 / T1 = P2
/ T2
This is the 2-point form of Gay-Lussac's (or Amonton's) Law. It
it used to relate the pressures and temperatures in two states that are
connected by a process that does not change the volume or number of moles.
4.4 The Combined Gas Law
So far, we have seen three 2-point gas laws. All of these require
that the number of moles of gas remain constant. In addtion, each
of these requires that one of the remining variables -- pressure, volume,
or temperature -- remain constant. But suppose we have a process
that changes the pressure, volume and temperature of a gas all at the same
time? Then none of the laws we have considered so far will help us.
There is another law we will consider that help us in such a case.
It is the combined gas law, and can be expressed in the form
P1 V1 / T1 =
P2 V2 / T2
Notice that the above equation will reduce to each of the three individual
gas laws when the appropriate variable is held constant. For example,
if the process is isothermal, temperature is constant. Then T1
= T2 = T. That is, we don't need a state label if the
temperatures are the same in both states. Then the equation becomes
P1 V1 / T = P2
V2 / T
and multiplying by T on both cancels out the T and leaves
P1 V1 = P2
V2
This is just the equation of Boyle's Law, which we had already seen
applies when temperature is constant (section 4.1). In the same way,
we could show that the combined gas law reduces to Charles' Law for an
isobaric (constant pressure) process and to Gay-Lussac's (or Amonton's)
Law for an isochoric (constant volume) process. There really is not
any need to do complicated algebra to show this. Just cover up (or
erase) the variable that is being held constant, and what remains is the
equation for the relevant individual gas law.
The only thing required to remain constant in the combined gas law (in
the form presented here) is the number of moles, since n does not appear
in the equation. Actually, we could remove this restriction by writing
it in the form
P1 V1 / n1 T1
= P2 V2 / n2 T2
but in General Chemistry, we are not likely to do calculations in which
the number of moles of gas changes during the process, so the simpler form
presented earlier (not containing n) will usually suffice.
4.5 Avogadro's Law
Avogadro's Law considers the relationship between the volume of a gas (at
fixed temperature and pressure) and the amount (number of moles) of gas.
We did not use it in deriving any of the 2-point laws, because we were
not interested in changing the number of moles during a process.
However, we will need this law to derive the Ideal Gas Law.
Avogadro's Law states that the volume of a gas (at
fixed temperature and pressure) is directly proportional to the number
of moles of gas. Mathematically, this can be expressed as V a
n. This is a fairly obvious law. Consider what happens when
you inflate a balloon. The more air you put in the balloon, the larger
the volume becomes.
5. The Ideal Gas Law
We now make use of some of the laws previously developed to derive the
Ideal Gas Law. Specifically, we will need the following:
V a 1 / P (Boyle's
Law)
V a T
(Charles' Law)
V a n
(Avogadro's Law)
If a single variable (V in this case) is proportional to several other
variables, it is proportional to their product. This allows several
individual proportionalities to be combined into a single proportionality.
The above can be combined to give
V a n T / P
In this proportionality, all gas parameters are present, so when we
make it into an equation, the constant of proportionality will be a true
universal constant. It will not depend on anything. As usual,
we will change the proportionality sign (a)
to an equality sign (=) and multiply the right hand side by a constant.
This time, we will call it R rather than k, to make our equation look like
that presented in standard general chemistry textbooks.
V = R n T / P
We can clear the fraction on the right side by multiplying both sides
by P. This gives
P V = n R T
(Ideal Gas Law)
The fact that I wrote n R T this time instead of R n T has no mathematical
consequence, since numbers can be multiplied in any order. This was
done to make our equation coincide with that presented in general chemistry
textbooks.
The value of R can be determined experimentally by simultaneously determining
for a known amount (number of moles) of gas, its pressure, temperature
and volume. Re-arranging the equation as
R = P V / n T
the measured values can be plugged into the equation to calculate R.
The currently accepted value of R is as follows:
R = 0.0820584 L atm / K mol
The Ideal Gas Law differs from all the laws presented before it in that
it applies to a one state problem. In using each of the other laws,
we were considering a gas in a particular initial state ("STATE 1") that
underwent some process that transformed it to some final state ("STATE
2"). In using the Ideal Gas Law, we will have a single state for
the gas, in which we know all of the variables except one. That missing
variable can be solved for algebraically.
Simple Ideal Gas Law problems will ask for the pressure, volume, or
temperature to be solved for. The re-arrangements to use for these
tasks are as follows:
P = n R T / V
(to solve for pressure)
V = n R T / P
(to solve for volume)
T = P V / n R
(to solve for Kelvin temperature)
Sometimes, we will need to solve for the number of moles of gas.
Usually, this will be done as part of a more elaborate problem, in which
calculating the number of moles is not the end result, but merely a step
on the way to the desired answer. When moles need to be calculated,
the following re-arrangement is used:
n = P V / R T
(to calculate the number of moles of gas)
5.1 Extensions of the Ideal Gas Law -- Variants of the Original Equation
In addition to the simple calculations of pressure, volume, and temperature
discussed in section 5 proper, there are additional calculations that may
be of interest that we now consider in this sub-section. Consider
the following questions:
-
A steel tank having a volume of 9.582 L contains N2 gas under
a pressure of 4.973 atm at 31.8 oC. What mass of N2
is in the tank?
-
What is the denisty of CH4 when kept under a pressure of 8.175
atm at 26.3 oC?
-
An unknown gas has a density of 3.429 g / L when the pressure is 2.593
atm and the temperature is 21.7 oC. What is the molecular
weight of this gas?
The parameters asked for in these equations -- mass, density, and molecular
weight -- do not appear explicitly in the Ideal Gas Law. However,
there are auxillary equations we can combine with the Ideal Gas Equation
to come up special versions of the equation to meet our needs.
Density is an elementary concept that is usually mentioned in the first
chapter of general chemistry textbooks. An object's density is its
mass divided by its volume.
d = m / V
Molecular weight is also a fairly simple concept to develop. When
you learned the mole concept, you were taught that one mole weighs in grams
what one molecule (at least on average -- if isotopes are a factor) weighs
on the atomic mass scale. That is, units of molecular weight are
either u/molecule or g/mole. Generally, the unit g/mole is more useful
to us. These units suggest that we can calculate the molecular weight
by dividing a substance's mass in grams by the number of moles it contains.
That is,
MWT = m / n
where MWT stands for molecular weight, m is the mass in grams and n
is the number of moles.
We shall now see how the above two simple equations can be combined
with the Ideal Gas Law to produce some useful variations on a theme.
5.1.1 The Mass-Based Ideal Gas Law
Suppose you want to answer a mass question like that posed in section 5.1.
Here is how you can get an equation containing the mass:
First, from the equation
MWT = m / n
solve for n to get
n = m / MWT
Then substitute this result into the Ideal Gas Law to get
P V = ( m / MWT ) R T
The fraction can be cleared by multiplying by MWT on both sides to get
P V (MWT) = m R T
(Mass-Based Ideal Gas Law)
With this equation, the mass of a known gas (i.e. one for which we know
the molecular weight) can be calculated directly, because the mass appears
explicitly in the equation.
5.1.2 The Density-Based Ideal Gas Law
To answer the second and third questions posed in section 5.1, we need
a form of the Ideal Gas Law in which the density appears explicitly in
the equation. We can derive such an equation as follows:
Starting from the Mass-Based Ideal Gas Law (derived in section 5.1.1)
P V (MWT) = m R T
Divide both sides by V to get
P (MWT) = (m / V) RT
Then recognizing that d = m / V, we can write
P (MWT) = d R T
(Density-Based Ideal Gas Law)
6. Dalton's Law of Partial Pressures
So far, we have considered pure gases. But often we have to work
with mixtures of gases. The air around us, for example, is a mixture
that consists of 78% N2, 21% O2, and 1% a mixture
of several gases. Each gas in a mixture occupies the same volume
as the mixture as a whole (all molecules are free to move throughout the
space available to the gas), and assuming uniform temperature distribution,
all gases in the mixture are at the same temperature. However, the
amount of each gas (number of moles) is probably not the same. Recall
that the pressure exerted by a gas in a container is the result of collisions
of the gas molecules with the container walls (section 1). Therefore,
the contribution that each gas makes to the total pressure in a container
will be proportional to the number of molecules (and therefore moles) of
that gas.
When more than one gas is present in a container, each gas is said to
exert a partial pressure. The total pressure exerted by the
gas mixture (the pressure we would measure with a mechanical pressure meter)
is equal to the sum of the partial pressures of each of the gases making
up the mixture. That is,
PT = P1 +
P2 + . . . . .
where PT is the total gas pressure, P1 is the
partial pressure of gas 1, P2 is the partial pressure of gas
2, and so on. The sum extends over all the gases in the mixture.
Dalton's Law could be used to answer a question like the following:
-
A steel tank having a volume of 7.163 L contains 4.973 g of N2
and 6.851 g of O2 at 28.4 oC. What pressure
is exerted by this gas mixture?
This could be solved in either of 2 ways. The method that emphasizes
Dalton's Law is to calculate the partial pressure of each gas separately
-- in the usual way, using the Ideal Gas Law. Each gas exerts the
same pressure as it would exert if it were alone in the container.
The partial pressures would then be added to obtain the total pressure.
A second way to solve this problem would be to add the number of moles
of the two gases to get the total number of moles of gas in the container,
then calculate the pressure corresponding to that number of moles.
This procedure works because the pressure of a gas is determined by the
number of moles in its volume, without regard to the chemical identity
of the gas. On a molar bases, all gases make the same contribution
to the pressure. (This is assuming ideal gas behavior.)
7. Graham's Law of Effusion
Because gas molecules are in constant random motion, two (or more) initially
pure gases that share the same container will soon become thoroughly mixed.
This bulk mixing of gases is called diffusion. Diffusion accounts
for the fact that when dinner is being cooked in the kitchen, the aroma
can soon be detected throghout the house. Molecules of the substances
responsible for the aroma work their way through the "jungle" of molecules
that make up the air, so that those molecules that at first were only in
the kitchen are now all over the house.

While diffusion is easy to understand in a qualitative way, mathematical
calculations are extermely difficult because of the large number of collisions
that the molecules undergo as they mix. Effusion, like diffusion,
is related to molecular motion, but is much easier to describe mathematically.
Effusion
is the escape of a gas through a small hole, having a size similar
to the gas molecules themselves. While diffusion refers to a
bulk mixing of gases, effusion involves the escape of gas molecules essentially
one-by-one from the container.
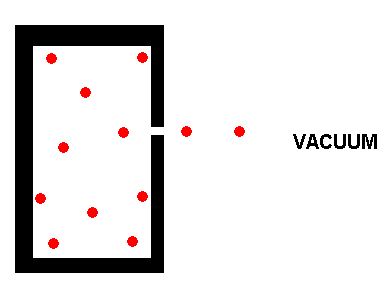
In the above container, a gas molecule can escape if it is moving toward
the hole. An individual gas molecule will usually have to undergo
numerous collisions with the walls of the container, and with other gas
molecules, before it happens to be moving in the right direction to allow
it to pass through the hole. Because of the small size of the hole,
only one molecule at at time (or at most just a few at a time), can pass
through the hole. Effusion is therefore, a slow process. A
large hole would allow the gas to escape from the container rapidly, but
this would be bulk movement of gas, and not effusion.
In describing effusion mathematically, we usually consider the space
outside the container to be a large volume of vacuum. With this assumption,
it is not likely that a molecule will ever return to the container once
it leaves, so we only need to consider the movement of gas molecules out
of
the hole. We will only have gas leaving the container, none entering.
The rate at which gas molecules escape from the container will be related
to their speed. This in turn, will depend on two things: the temperature
and the mass of the molecule. The higher the temperature, the faster,
on average, the molecules are moving. And at a given temperature,
the heavier the molecule is, the slower it moves. In comparing the
effusion rates of two different gases, we usually compare them at the same
temperature. This allows us to confine our attention to the mass
of the molecule. Graham's Law of Effusion states that at
a given temperature and pressure, the effusion rate of gas is inversely
proportional to the square root of its molecular weight. Mathematically,
this can be expressed as:
Effusion Rate a 1/Ömolecular
weight
If we apply this equation to two different gases, which we will call
gas 1 and gas 2, we can obtain the following equation for comparing the
two gases:
E.R. 1 / E.R. 2 = Ö
(
MWT 2 / MWT 1 )
Where E.R. is the effusion rate and MWT is the molecular weight.
The labels 1 and 2 indicate which gas is being dealt with.
Since the time required for a gas to effuse will be inversely proportional
to its effusion rate, we can also write an equation that lets us compare
two gases on the basis of their effusion times:
E.T. 1 / E.T. 2 = Ö
(
MWT 1 / MWT 2 )
This equation will allow us to answer questions like the following:
-
If it takes 50.76 minutes for CO2 effuse through a small hole
in its container, how long will it take for NH3 to effuse under
the same conditions of temperature and pressure?
-
An unknown gas effuses out of its container in 60.0 minutes. Under
the same conditions of temperature and pressure, helium requires 30.0 minutes.
What is the molecular weight of the unknown gas?
7. Stoichiometry of Gas Reactions
When a chemical reaction involves gases, we may want to calculate the volume
of a gas that can be produced by a chemical reaction, or the gas pressure
that may be developed by a chemical reaction. This will depend on
both the amount of gaseous substance that can be produced (a stoichiometry
problem) and the conditions under which the gas is being produced (a gas
law probelm). Thus problems of this type must be solved in two parts.
First, we must do a stoichiometric calculation to determine how many moles
of gas we can produce. Then, we must use the ideal gas law to calculate
the pressure or volume, as appropriate, for the number of moles of gas
that have been produced.
8. Some Representative Gas Calculations
8.1 Boyle's Law
A gas was confined in a cylinder fitted with a movable piston. At
21.4 oC, the gas occupied a volume of 6.183 L under a pressure
of 1.997 atm. The gas was isothermally compressed to volume of 4.208
L. What pressure was exerted by the compressed gas?

V1 = 6.183 L
V2 = 4.208 L
P1 = 1.997 atm
P2 = ?
P1 V1 = P2
V2 -----solve----->
P2 = P1 ( V1 / V2 )
P2 = 1.997 atm ( 6.183 L / 4.208 L ) = 2.934 atm
A gas was confined in a cylinder fitted with a movable piston.
At 21.8 oC, the gas occupied a volume of 4.342 L under a pressure
of 2.075 atm. The gas was isothermally compressed, increasing its
pressure to 3.317 atm. What volume was occupied by the compressed
gas?

V1 = 4.342 L
V2 = ?
P1 = 2.075 atm
P2 = 3.317 atm
P1 V1 = P2
V2 -----solve----->
V2 = V1 ( P1 / P2 )
V2 = 4.342 L ( 2.075 atm / 3.317 atm ) = 2.716 L
8.2 Charles' Law
A gas was confined in a cylinder fitted with a movable piston. At
15.2 oC, the gas occupied a volume of 7.884 L. under a
pressure of 1.318 atm. The gas was isobarically heated causing it
to expand to a volume of 9.023 L. What was the temperature -- in
degrees Celsius -- of the heated gas?

V1 = 7.884 L
V2 = 9.023 L
T1 = 15.2 oC
T2 = ?
= 288.35 K
V1 / T1 = V2
/ T2 -----solve----->
T2 = T1 ( V2 / V1 )
T2 = 288.35 K ( 9.023 L / 7.884 L ) = 330.01
K = 56.9 oC
A gas was confined in a cylinder fitted with a movable piston.
At 20.3 oC, the gas occupied a volume of 5.984 L under a pressure
of 1.327 atm. The gas was isobarically heated to a temperature of
99.8 oC. What was the volume of the hot gas?

V1 = 5.984 L
V2 = ?
T1 = 20.3 oC
T2 = 99.8 oC
= 293.45 K
= 372.95 K
V1 / T1 = V2
/ T2 -----solve----->
V2 = V1 ( T2 / T1 )
V2 = 5.984 L ( 372.95 K/ 293.45 K ) = 7.605
L
8.3 Gay-Lussac's (Amonton's) Law
A gas was confined in a steel tank having a volume of 6.982 L. At
19.7 oC, the gas exerted a pressure of 7.532 atm. The
gas was heated, causing the pressure to increase to 9.406 atm. What
was the temperature of the hot gas?

P1 = 7.532 atm
P2 = 9.406 atm
T1 = 19.7 oC
T2 = ?
= 292.85 K
P1 / T1 = P2
/ T2 -----solve----->
T2 = T1 ( P2 / P1 )
T2 = 292.85 K ( 9.406 atm / 7.532 atm ) = 365.71
K = 92.6 oC
A gas was confined in a steel tank having a volume of 5.874 L.
At 18.5 oC, the gas exerted a pressure of 7.214 atm. The
gas was heated to a temperature of 87.3 oC. What pressure
was exerted by the hot gas?

P1 = 7.214 atm
P2 = ?
T1 = 18.5 oC
T2 = 87.3 oC
= 291.65 K
= 360.45 K
P1 / T1 = P2
/ T2 -----solve----->
P2 = P1 ( T2 / T1 )
P2 = 7.214 atm ( 360.45 K / 291.65 K ) = 8.916
atm
8.4 Combined Gas Law
A gas was confined in a cylinder fitted with a movable piston. At
21.4 oC, the gas occupied a volume of 6.184 L under a pressure
of 2.225 atm. The gas was simultaneously heated and compressed, so
that its temperature was 91.8 oC and its pressure was 4.806
atm. What volume was occupied by the hot compressed gas?

V1 = 6.184 L
V2 = ?
P1 = 2.225 atm
P2 = 4.806 atm
T1 = 21.4 oC
T2 = 91.8 oC
= 294.55 K
= 364.95 K
P1 V1 / T1 =
P2 V2 / T2 -----solve----->
V2 = V1 ( P1 / P2 ) ( T2
/ T1 )
V2 = 6.184 L (2.225 atm / 4.806 atm ) ( 364.95 K /
294.55 K ) = 3.547 L
A gas was confined in a cylinder fitted with a movable piston.
At 22.6 oC, the gas occupied a volume of 9.112 L under a pressure
of 2.046 atm. The gas was simultaneously heated and compressed, so
that its temperature was 94.2 oC and its volume was 4.543 L.
What pressure was exerted by the hot compressed gas?

V1 = 9.112 L
V2 = 4.543 L
P1 = 2.046 atm
P2 = ?
T1 = 22.6 oC
T2 = 94.2 oC
= 295.75 K
= 367.35 K
P1 V1 / T1 =
P2 V2 / T2 -----solve----->
P2 = P1 ( V1 / V2 ) ( T2
/ T1 )
P2 = 2.046 atm ( 9.112 L / 4.543 L ) ( 367.35 K /
295.75 K ) = 5.097 atm
A gas was confined in a cylinder fitted with a movable piston.
At 15.4 oC, the gas occupied a volume of 6.947 L under a pressure
of 3.858 atm. The gas was simultaneously heated and compressed, which
reduced its volume to 4.178 L and increased its pressure to 8.071 atm.
What was the temperature -- in degrees Celsius -- of the hot compressed
gas?

V1 = 6.947 L
V2 = 4.178 L
P1 = 3.858 atm
P2 = 8.071 atm
T1 = 15.4 oC
T2 = ?
= 288.55 K
P1 V1 / T1 =
P2 V2 / T2 -----solve----->
T2 = T1 ( P2 / P1 ) ( V2
/ V1 )
T2 = 288.55 K ( 8.071 atm / 3.858 atm ) ( 4.178 L
/ 6.947 L ) = 363.04 K = 89.9 oC
8.5 Ideal Gas Law
What pressure is exerted by 7.898 g of CH4 in a 5.943 L tank
at 28.5 oC?
METHOD 1:
7.898 g CH4 ( 1 mol CH4 / 16.04 g CH4
) = 0.4923 mol CH4
P V = n R T -----solve----->
P = n R T / V
P = 0.4923 mol (0.0820584 L atm / K mol ) ( 301.65 K ) / 5.943
L
P = 2.050 atm
METHOD 2:
P V (MWT) = m R T -----solve----->
P = m R T / ( V . MWT )
P = 7.898 g (0.0820584 L atm / K mol ) (301.65 K ) / ( 5.943
L . 16.04 g / mol )
P = 2.050 atm
Note: numbers shown in the calculations have been rounded
off to conserve space, but the full unrounded values were used to carry
out the calculations.
A steel tank contains 8.853 g of O2 gas under a pressure
of 4.957 atm at 22.9 oC. What is the volume of the tank?
METHOD 1:
8.853 g O2 ( 1 mol O2 / 32.00 g O2
) = 0.2767 mol O2
P V = n R T -----solve----->
V = n R T / P
V = 0.2767 mol (0.0820584 L atm / K mol ) ( 296.05 K ) / 4.957 atm
V = 1.356 L
METHOD 2:
P V (MWT) = m R T -----solve----->
V = m R T / ( P . MWT )
V = 8.853 g (0.0820584 L atm / K mol ) (296.05 K ) / ( 4.957 atm .
32.00 g / mol )
V = 1.356 L
Note: numbers shown in the calculation have been rounded
off to conserve space, but the full unrounded values were used to carry
out the calculations.
A steel tank having a volume of 5.821 L contains 8.782 g of O2
under a pressure of 1.353 atm. What is the temperature -- in degrees
Celsius -- of the O2?
METHOD 1:
8.782 g O2 ( 1 mol O2 / 32.00 g O2
) = 0.2744 mol O2
P V = n R T -----solve----->
T = P V / ( n R )
T = 1.353 atm (5.821 L ) / ( 0.2744 mol . 0.0820584
L atm / K mol )
T = 349.71 K = 76.6 oC
METHOD 2:
P V (MWT) = m R T -----solve----->
T = P V (MWT) / m R
T = 1.353 atm ( 5.821 L ) ( 32.00 g / mol ) / ( 8.782 g .
0.0820584 L atm / K mol )
T = 349.71 K = 76.6 oC
Note: numbers shown in the calculation have been rounded
off to conserve space, but the full unrounded values were used to carry
out the calculations.
A steel tank having a volume of 9.582 L contains N2 gas
under a pressure of 4.973 atm at 31.8 oC. What mass of
N2 is in the tank?
METHOD 1:
P V = n R T -----solve----->
n = P V / ( R T )
n = 4.973 atm ( 9.582 L ) / ( 0.0820584 L atm / K mol .
304.95 K )
n = 1.904 mol
1.904 mol N2 ( 28.01 g N2 / mol N2
) = 53.34 g N2
METHOD 2:
P V (MWT) = m R T -----solve----->
m = P V (MWT) / ( R T )
m = 4.973 atm ( 9.582 L ) ( 28.01 g / mol ) / ( 0.0820584 L atm / K
mol . 304.95 )
m = 53.34 g
Note: numbers shown in the calculation have been rounded
off to conserve space, but the full unrounded values were used to carry
out the calculations.
What is the denisty of CH4 when kept under a pressure of
8.175 atm at 26.3 oC?
METHOD 1:
Assume a volume of 1L.
P V = n R T -----solve----->
n = P V / ( R T )
n = 8.175 atm ( 1 L ) / ( 0.0820584 L atm / K mol .
299.45 K )
n = 0.3327 mol
0.3327 mol CH4 ( 16.04 g CH4 / 1 mol CH4
) = 5.337 g CH4
d = m / V = 5.337 g / 1 L =
5.337 g / L
METHOD 2:
P (MWT) = d R T -----solve----->
d = P (MWT) / ( R T )
d = 8.175 atm ( 16.04 g / mol ) / ( 0.0820584 L atm / K mol .
299.45 K )
d = 5.337 g / L
Note: numbers shown in the calculation have been rounded
off to conserve space, but the full unrounded values were used to carry
out the calculations.
An unknown gas has a density of 3.429 g / L when the pressure is 2.593
atm and the temperature is 21.7 oC. What is the molecular
weight of this gas?
METHOD 1:
Assume a volume of 1 L. The mass of gas in this volume will be
3.429 g, as shown below:
3.429 g / L ( 1 L ) = 3.429 g
P V = n R T -----solve----->
n = P V / ( R T )
n = 2.593 atm ( 1 L ) / ( 0.0820584 L atm / K mol .
294.85 K )
n = 0.1072 mol
MWT = m / n = 3.429
g / 0.1072 mol = 32.00 g / mol
METHOD 2:
P (MWT) = d R T -----solve----->
MWT = d R T / P
MWT = ( 3.429 g / L ) ( 0.08205783 L atm / K mol ) ( 294.85 K
) / 2.593 atm
MWT = 32.00 g / mol
Note: numbers shown in the calculation have been rounded
off to conserve space, but the full unrounded values were used to carry
out the calculations.
8.6 Dalton's Law of Partial Pressure
A steel tank having a volume of 7.163 L contains 4.973 g of N2
and 6.851 g of O2 at 28.4 oC. What pressure
is exerted by this gas mixture?
METHOD:
Calculate the moles of each gas, then calculate the (partial) pressure
of each gas in the usual way. A gas in a mixture exerts the same
pressure as it would exert if it were alone in the container.
4.973 g N2 ( 1 mol N2 / 28.01 g N2
) = 0.1775 mol N2
6.851 g O2 ( 1 mol O2 / 32.00 g O2
) = 0.2141 mol O2
P V = n R T -----solve----->
P = n R T / V
For N2 : P = 0.1775 mol ( 0.0820584 L atm / K mol )
( 301.55 K ) / 7.163 L
P = 0.6133 atm
For O2 : P = 0.2141 mol ( 0.0820584 L atm / K
mol ) ( 301.55 K ) / 7.163 L
P = 0.7396 atm
PTOTAL = 0.6133 atm +
0.7396 atm = 1.3529 atm
You can also calculate the total gas pressure from the total gas moles:
Total moles = 0.1775 mol +
0.2141 = 0.3916 mol
P = 0.3916 mol ( 0.0820584 L atm / K mol ) ( 301.55 K ) / 7.163
L
P = 1.3529 atm
Note: numbers shown in the calculation have been rounded
off to conserve space, but the full unrounded values were used to carry
out the calculations.
8.7 Graham's Law of Effusion
If it takes 50.76 minutes for CO2 effuse through a small hole
in its container, how long will it take for NH3 to effuse under
the same conditions of temperature and pressure?
METHOD:
We will use the equation
E.T. 1 / E.T. 2 = Ö
(
MWT 1 / MWT 2 )
Let's let NH3 be gas 1 and CO2 be gas 2.
This will put the quantity we are trying to solve for in the numerator.
This is not a requirement, but solving for a numerator quantity tends to
be easier and less error-prone than solving for a denominator quantity.
Making the equation specific to our particular problem, we have
E.T. NH3 / E.T. CO2 = Ö
(
MWT NH3 / MWT CO2 )
Solving this for E.T. NH3 we have
E.T. NH3 = ( E.T. CO2 ) Ö
(MWT
NH3 / MWT CO2 )
and substituting values we have
E.T. NH3 = 50.76 min Ö
( (17.03 g / mol ) / ( 44.01 g / mol )
)
E.T. NH3 = 31.58 min
Note: numbers shown in the calculation have been rounded
off to conserve space, but the full unrounded values were used to carry
out the calculations.
An unknown gas effuses out of its container in 60.0 minutes.
Under the same conditions of temperature and pressure, helium requires
30.0 minutes. What is the molecular weight of the unknown gas?
METHOD:
We will use the equation
E.T. 1 / E.T. 2 = Ö
(
MWT 1 / MWT 2 )
Let's let the unknown gas be gas 1 and helium be gas 2. This will
place the variable being solved for in the numerator, which is preferred
(see previous problem). Making the equation specific to our particular
problem, we have
E.T. unknown / E.T. He = Ö
( MWT unknown / MWT He )
Squaring both sides of the equation (and writing the variable being
solved for one the left hand side this time, we have
MWT unknown / MWT He = ( E.T. unknown / E.T.
He )2
Then multiplying both sides by MWT He gives
MWT unknown = MWT He ( E.T. unknown / E.T. He
)2
and substituting the numerical values into this equation gives
MWT unknown = ( 4.0026 g / mol )
( 60.0 min / 30.0 min )2
MWT unknown = 16.0 g / mol
Note: numbers shown in the calculation have been rounded
off to conserve space, but the full unrounded values were used to carry
out the calculations.
8.8 Stoichiometry of Gas Reactions
Oxygen gas can be prepared by the thermal decomposition of potassium chlorate,
a white solid. What volume (in mL) of oxygen gas can be produced
under STP conditions by the thermal decomposition of 0.500 g of potassium
chlorate? (In addition to oxygen gas, solid potassium chloride is
also a decomposition product.)
METHOD:
First, we will need to come up with a balanced equation for the reaction
so we can do a stoichiometric calculation of the number of moles of oyxgen
we can produce. Then we can use the Ideal Gas Law to calculate the
volume that should be occupied by this oxygen.
potassium chlorate ----------> potassium chloride
+ oxygen
KClO3(s) ----------> O2(g)
+ KCl(s)
(unbalanced)
2KClO3(s) ----------> 3O2(g)
+ 2KCl(s) (balanced)
0.500 g KClO3 ( 1 mol KClO3 / 122.5 g KClO3
) ( 3 mol O2 / 2 mol KClO3 ) = 0.006120 mol
O2
P V = n R T ----solve----->
V = n R T / P
STP conditions are 0 oC (which is 273.15 K) and 1 atm.
V = 0.006120 mol ( 0.0820584 L atm / K mol ) ( 273.15 K ) / 1 atm
V = 0.137 L
0.137 L ( 1 mL / 1 x 10-3 L ) =
137 mL
Note: numbers shown in the calculation have been rounded
off to conserve space, but the full unrounded values were used to carry
out the calculations.
Last update: Friday December 1, 2000