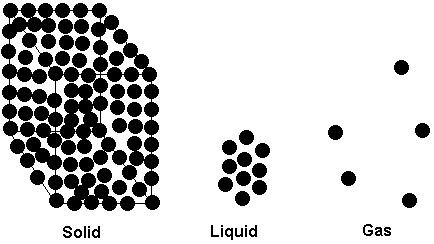
In these notes, we look at the three states of matter, their physical properties, and conversions from one state to another. Macroscopically, we all know what the 3 states of matter look like. Solids have a definite size and shape. Liquids have a definite size but no definite shape. A liquid will take the shape of the container it occupies. Gases have neither a definite size nor a definite shape. Like a liquid, a gas will take the shape of its container, but unlike a liquid, a gas will expand to fill a container of any size. Of course, as a gas expands to fill a container of large volume, the pressure of the gas decreases. You may recall that we looked at the relationship between the volume and the pressure of a fixed amount of gas (at constant temperature) in General Chemistry I. The relationship was found to be an inverse proportionality and was known as Boyle's Law.
At the microscopic level, we picture the differences between the states of matter as being due to the spacing and freedom of mobility of the particles (molecules, atoms, ions, as the case may be, depending on what substance is under consideration) of which the substance is composed.

The reason a solid has a definite size and shape is that its particles occupy fairly rigid positions in space. Although they do have some mobility (with the possible exception of a system at a temperature of zero Kelvin, which we can never attain anyway), that mobility is of a vibrational nature -- that is, the particles oscillate back and forth around a central or equilibrium position. There is no long range motion. The particles are also quite close together, so there is little room available to squeeze them any closer together. This is what gives solids their incompressibility. In a liquid the particles are also close together, but they are not held in fixed positions as they are in a solid. As a result, a liquid exhibits a property known as fluidity -- the ability to flow. It is the ability of the particles to change their relative positions that gives a liquid its fluidity, and its ability to take the shape of whatever container it occupies. Because the particles remain close together in a liquid, liquids, like solids, are incompressible. In gases, the molecules are, on average, separated by distances that are quite large in comparison to the size of the particles themselves. A gas is mostly empty space. Although we often think of the term "fluid" as another word for "liquid", gases are fluids also. A fluid is merely something that has the ability to flow, and gases certainly have this property. Unlike solids and liquids, gases are highly compressible. There is a lot of space between the molecules of a gas, which means a lot of space available for the molecules to be pushed closer together. Thus, when we increase the pressure on a gas, the volume is significantly reduced, while increasing the pressure on a solid or liquid has minimal effect.
You may recall that in General Chemistry I, that we were able to derive an equation called the Ideal Gas Law, PV=nRT, which treated all gases the same. We used that equation to solve problems involving a wide variety of gases. However, there is no counterpart to this equation for solids and liquids -- no Ideal Solid Law or Ideal Liquid Law. This is due to differences in the strength of the intermolecular attractive forces in the three states of matter. Later in these notes, we will look at the nature of the attractive forces that exist between molecules (which we shall use in a generic way to mean molecules, atoms, or ions as the case may be). For now, however, we only need to know that all molecules have at least a slight attractive force acting between them, and this force decreases rapidly with the distance of separation of the molecules. The strength with which molecules attract each other is determined by their chemical composition. In the case of a gas, however, the molecules are, on average, so far apart that they don't interact with each other. This means that differences in their inherent ability to attract each other have no effect on the properties of a gas. For solids and liquids, the molecules are close enough together that differences in the strengths of their attractive forces are significant, and have observable effect on their physical properties. Therefore, we can not treat solids and liquids with a "one size fits all" approach as we do for gases.
In Section 1, we looked at the spacing and freedom of mobility of the molecules in solids, liquids, and gases, and also noted that molecules attract each other. Let's keep those points in mind as we consider what happens when a solid is heated and eventually changed to a liquid and then a gas.
As a solid is heated, the vibrational motion of the molecules increases. When the vibrational energy becomes large enough, it overcomes the attractive forces that tend to hold the molecules in their fixed positions and the solid structure collapses, forming a liquid. We refer to this as melting or fusion. The temperature at which this happens is called the melting point. The melting point is slightly pressure dependent. We generally report a melting point under normal atmospheric pressure, which is 760 torr or 1 atm. Strictly speaking, we should refer to it as a normal melting point, but we often just say "melting point", and the pressure is assumed to be 760 torr unless specified otherwise. Even if the pressure is not 760 torr, the melting point is almost the same as the normal melting point because the melting point changes only slightly, even with large changes in pressure. The melting point is related to the strength of the intermolecular attractive forces in the solid. The stronger these forces are, the greater the vibrational energy the molecules must have to overcome the attractive forces and therefore, the higher the temperature required for melting. Melting is an example of a phase change, the conversion of a substance from one form to another. Here, the phase change is a change in state -- from the solid state to the liquid state. But not all phase changes necessarily involve changes in state. If a solid can exist in two different crystalline forms, those two forms correspond to different phases, even though both are in the solid state.
As the solid is melting, the temperature remains constant, even though we continue to add heat to the system. Melting, or fusion, is an endothermic process. While the solid is being melted, the heat being added is used to drive the endothermic fusion process, and it is therefore not available to raise the temperature of the system. In General Chemistry I, we looked at some elementary thermochemistry, and we learned the meaning of DH for a chemical reaction. Even though fusion is not a chemical reaction in the strictest sense (we still have the same substance), we can, nevertheless, write a thermochemical equation for it just as we did for chemical reactions that we encountered in General Chemistry I. Using water as an example, we can write the following:
H2O(s) ----------> H2O(l) ΔHfus = 6.02 kJ
The accompanying chemical reaction shows us that the value is for one mole of water. When we write the heat of fusion without also writing the chemical reaction, we usually report it as 6.01 kJ/mol to remind us that this value is for 1 mole. The numerical value of heats of fusion are given at the substances's normal melting point, which for water, is 0 oC. If we know a substance's heat of fusion, we can easily calculate the amount of heat required to melt a specified amount of the substance at its melting point. For example, if we wanted to melt 50.0 g of ice at 0 oC, we would calculate the amount of heat as follows:
1 mol 6.02 kJ
50.0 g x --------- x
-------- = 16.7 kJ
18.02 g 1 mol
If the solid starts out below its melting point, we must also consider the heat needed to warm up the solid to its melting point. For example, suppose the 50.0 g of ice started out at -10.0 oC. In order to melt it, we would first need to warm it up from -10.0 o C to 0.0 oC. Only after the ice had reached 0.0 oC could we begin to melt it. Given that the specific heat capacity of ice is 2.00 J/goC, the amount of heat required for the warming process would be
2.09 J
------- x 50.0 g x 10.0 oC
= 1045 J =
1.045 kJ
g oC
The above calculation makes use of the formula q = s . m . Δt which you learned about in General Chemistry I. We calculate the heat by multiplying the specific heat, the mass, and the desired temperature change. In this example, we want to raise the temperature of the ice from -10.0 oC to 0.0 oC, a change of 10.0 oC. The total required heat for warming the ice and then melting it is
Total heat = 1.045 kJ
+ 16.7 kJ = 17.745 kJ »
17.7 kJ
warming ice melting ice
Going back to our generic heating discussion, once we have melted all of the solid, the temperature will begin to rise again as we continue adding heat to the system. Now that a phase transition is no longer taking place, the added heat is "used" to increase the kinetic energy of the molecules in the now entirely liquid system. As heat continues to be added, the kinetic energy of the molecules continues to increase until it becomes large enough to overcome the attractive forces that hold the molecules close together in the liquid. At this point, molecules escape from the liquid and become gas molecules. Macroscopically, we observe that the liquid is boiling. The temperature at which this occurs is called the boiling point. If the liquid is being boiled under normal atmospheric pressure (760 torr or 1 atm) it is called the normal boiling point. Boiling points are highly dependent on pressure, far more so than melting points, for which the effect of pressure was almost negligible. As before, the qualifier "normal" is often assumed when it is not stated. Thus, when someone says "boiling point", they probably mean "normal boiling point". However, if the pressure is not 760 torr, the boiling point may differ markedly from its value at 760 torr.
Boiling is another example of a phase change. Here, it is a change in form from the liquid state to the gas state. Vaporization, like fusion, is an endothermic process. Heat put into the system to boil the liquid is used to overcome the attractive forces holding the molecules in the liquid. This heat is therefore not available to increase the kinetic energy of the molecules. As a result, temperature -- which is a measure of the average kinetic energy of the molecules -- remains constant. We can write a thermochemical equation for the vaporization of a liquid, just as we did for the melting of a solid. If the liquid being boiled is water, we can write the following:
H2O(l) ----------> H2O(g) ΔHvap = 40.7 kJ
The chemical equation shows us that the value is for 1 mole of water. If the value is reported without the accompanying equation, we should write it as 40.7 kJ/mol. The ΔH value reported here applies at water's normal boiling point of 100 oC. We can carry out thermochemical calculations for vaporization just as we did for fusion. Earlier we calculated the amount of heat needed to melt 50.0 g of ice at its melting point. The amount of heat needed was 16.7 kJ. Now let's calculate the amount of heat needed to vaporize (in this case, boil) 50.0 g of water at its normal boiling point.
1 mol
40.7 kJ
50.0 g x --------- x
--------- = 113 kJ
18.02 g 1 mol
Notice that the amount of heat needed for vaporization (113 kJ) is considerably greater than that needed for fusion (16.7 kJ). This seems reasonable when we consider the nature of these two processes at the molecular level. When a solid is melted, we disrupt the attractive forces that hold the molecules in their fixed positions in the solid. However, the molecules are still close together in the liquid and still have considerable attractive forces acting between them. Not all of the attractive forces need to be overcome to melt a solid. However, when a liquid is converted to a gas, virtually all the attractive forces have to be overcome. In a gas, the molecules are spread so far apart that they hardly interact at all. It takes more energy to achieve the molecular separations needed to convert a liquid to a gas than it does to convert a solid to a liquid. Therefore, heats of vaporization are expected to be greater than heats of fusion.
We have previously calculated the amount of heat needed to warm 50.0 g of ice from -10.0 oC to 0.0 oC, the amount of heat need to melt 50.0 g of ice, and the amount of heat needed to boil (vaporize) 50.0 g of water. If we want to consider the entire process of converting 50.0 g of ice at -10.0 oC to steam at 100.0 oC, we still need to calculate the amount of heat required to warm the water from 0 oC to 100 oC. When the ice is melted, we get water at 0 oC, and we can't boil it until it reaches 100 oC. Given that the specific heat of water is 4.18 J/goC, the calculation is carried out as follows:
4.18 J
-------- x 50.0 g x 100.0 oC
= 20900 J = 20.9
kJ
g oC
The total heat needed to convert 50.0 g of ice at -10.0 oC to steam at 100.0 oC is the sum of the heats for warming the ice, melting the ice, warming the water, and boiling the water.
Total heat = 1.045 kJ
+ 16.7 kJ + 20.9 kJ
+ 113 kJ = 151.6 kJ = 152 kJ
warming
melting
warming boiling
ice
ice
water
water
Once all the liquid has vaporized, continued heating will again raise the temperature as the heat is now available to increase the kinetic energies of the molecules in the now entirely gaseous system. In our sample calculations, we began with ice at a temperature that was 10.0 degrees below its normal melting point. So let's end this example by heating the steam to a temperature 10.0 oC above water's normal boiling point -- that is, let's heat the steam to 110.0 oC. Given that the specific heat of steam is 1.99 J/goC, the calculation is carried out as follows:
2.01 J
-------- x 50.0 g x 10.0 oC
= 1005 J =
1.005 kJ
g oC
This adds one more term to the sum of the heats. The total heat for the entire process of converting 50.0 g of ice at -10.0 oC to steam at 110.0 oC is calculated as follows:
1.045 kJ + 16.7 kJ
+ 20.9 kJ + 113 kJ +
1.005 kJ = 152.65 kJ = 153 kJ
warming
melting
warming
boiling
warming
ice
ice
water
water
steam
If we prepared a graph of our data for the heating experiment described here, it would look like the following:

The graph's features have each been labeled with a number. Here is what is happening in each numbered region:
Region 1: Ice is being warmed
Region 2: Ice is melting
Region 3: Water is being warmed
Region 4: Water is boiling
Region 5: Steam is being warmed
Now suppose we reverse the process. That is, we take the steam at 110.0 oC and cool it, eventually ending up with ice at -10.0 oC. In that case, we get a graph that is the reverse of the one shown above. It would look like this:
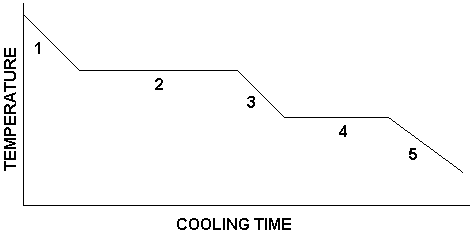
Here, the processes taking place in each numbered region are as follows:
Region 1: Steam is being cooled
Region 2: Steam is condensing
Region 3: Water is being cooled
Region 4: Water is freezing
Region 5: Ice is being cooled
In considering the heating experiment, we explained the temperature plateaus that accompanied melting and boiling (Regions 2 and 4, respectively, on the heating graph) as being due to the absorption of heat by the endothermic phase changes. This kept the heat from being available to raise the temperature of the system. We learned in General Chemistry I that the sign of DH changes when the direction of a chemical reaction is reversed. We have treated phase changes as "chemical reactions" for thermodynamic purposes, so if melting is endothermic, freezing must be exothermic. Likewise, if boiling (vaporization) is endothermic, condensation must be exothermic. For the condensation of steam and freezing of water, we can write the following thermochemical equations:
H2O(g) ----------> H2O(l) ΔH = -ΔHvap = -40.7 kJ
H2O(l) ----------> H2O(s) ΔH = -ΔHfus = -6.01 kJ
The amounts of heat involved in the phase changes are the same as before, but are heat releases rather than heat absorptions. These heat releases offset the heat being taken away from the system in the cooling process, so condensation and freezing occur at constant temperature, just as boiling and melting do.
We usually think of solids becoming liquids before they become gases. However, sometimes solids change directly to gases without going through the liquid state. This process is called sublimation, and we say the solid sublimes. "Dry ice" is an example with which you may be familiar. Dry ice is solid carbon dioxide. When heated under normal atmospheric pressure, it sublimes to the gas state without ever melting. The submimation takes place at -78 oC at normal atmospheric pressure, so dry ice can be used to refrigerate perishable items to colder temperatures than are possible with conventional water ice, and no unwanted liquid "waste" is generated in the process. The reverse of sublimation -- the conversion of a gas to a solid without becoming a liquid first -- is called deposition. In a later section of these notes, we shall consider all of these phase changes with the aid of a graph called a phase diagram.
Water can be vaporized by boiling, but it can also evaporate without being boiled. Wet clothing hung out on a clothesline will dry, but the water is not boiling in this case. Chemically speaking, we say the water evaporates. If a liquid (or a solid that sublimes) is placed in a closed container, it will fill the container with the gaseous form of the substance The partial pressure of this gas (or total pressure, if it is the only gas in the container) -- after it stabilizes -- is called the equilibrium vapor pressure. To visualize the establishment of equilibrium vapor pressure, let's consider a liquid placed into an evacuated container and allowed to vaporize. Initially, there exists a vacuum above the liquid, but molecules on the liquid's surface which have sufficient kinetic energy may overcome the attractive forces holding them in the liquid. These molecules will leave the surface and enter the space above the liquid to populate it with gas molecules. If the evaporation process takes place at constant temperature (we allow heat to flow into the system as necessary, to offset the heat absorbed by the endothermic vaporization process) the evaporation will occur at a constant rate. As the space above the liquid becomes populated with gas molecules, some of these molecules may collide with the liquid surface and get trapped there. This corresponds to condensation of the gas. The condensation rate will be proportional to the number of gas molecules per unit volume. The greater the number of gas molecules in a given volume (that is, the more crowded they are) the more often a gas molecule will collide with the liquid surface and get stuck there. When the liquid is first introduced into the vacuum, the condensation rate is zero, because no molecules have populated the gas space yet. As the evaporation proceeds, more and more molecules accumulate in the space above the liquid, and the condensation rate increases. Eventually, a point is reached at which the condensation rate has become equal to the evaporation rate. Once this happens, the number of gas (and liquid) molecules remains constant. This equilibrium, like all other chemical equilibria, is dynamic. That is, the evaporation and condensation processes continue to occur, but because they occur at the same rate, the macroscopic properties of the system remain constant. The vapor pressure that exists at this point is the equilibrium vapor pressure.
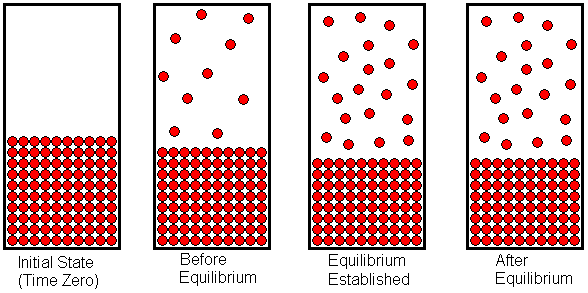
The establishment of equilibrium vapor pressure is shown in the diagram above. The state of the system is drawn at four different points in time. At the left end of the diagram, we see the liquid in a closed container with a vacuum above the liquid. As the liquid evaporates, the space above the liquid becomes populated with gas molecules. As we progress from left to right across the diagram, we see the state of the system at later and later times. In the second drawing, some of the liquid has evaporated, and the space above the liquid contains the gaseous form of the substance. At this point, evaporation is still occurring faster than condensation, so there is a net in-flux of molecules into the space above the liquid. In the third drawing, the gas molecules have become crowded enough that condensation occurs as fast as evaporation. When this conditions is first reached, equilibrium has been established. Once equilibrium has been established, the system will remain in equilibrium unless something is done to disrupt that equilibrium. The fourth drawing shows the state of the system at some time after the establishment of equilibrium. Notice that the system is no different than when it first reached equilibrium. Although some of the individual molecules may have exchanged roles (i.e., a particular gas molecule has become a liquid molecule, or a particular liquid molecule has become a gas molecule), the number of molecules in each state remains constant.
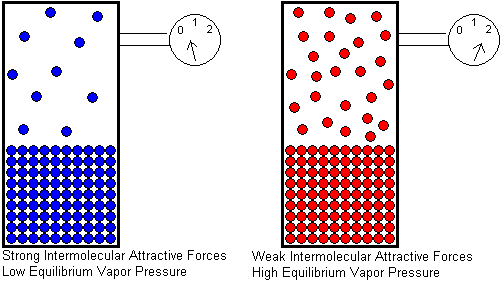
The equilibrium vapor pressure of a substance depends on two factors: the temperature and the strength of its intermolecular attractive forces. In order for a molecule to escape from a liquid, it must overcome the attractive forces that hold it in the liquid. Temperature is a measure of the average kinetic energy of the molecules. The higher the temperature, the greater the fraction of molecules that will have enough energy to escape from the liquid, and therefore, the greater the number of gas molecules per unit volume. More gas molecules in a given volume will generate a higher gas pressure, because the pressure of a gas results from collisions of the gas molecules with the container walls.
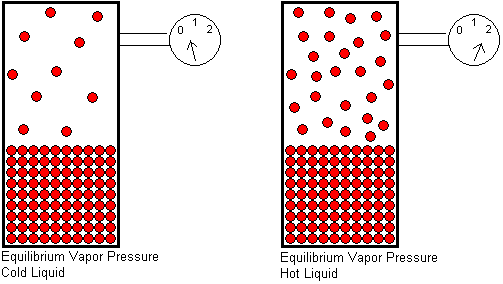
At any given temperature, if we compare the equilibrium vapor pressures of two different liquids, the liquid with stronger intermolecular attractive forces will have the lower equilibrium vapor pressure. The stronger the attractive forces, the greater the kinetic energy a molecule must have in order to escape from the liquid. A smaller fraction of molecules will be able to escape if the attractive forces are strong, and this will result in a lower equilibrium vapor pressure.
There are other factors we might consider which do not affect equilibrium vapor pressure, though at first glance, we might think they do. These factors are:
The surface area of the liquid
The volume of liquid in the container
The volume of the container
Students sometimes have the misconception that a liquid will have a higher equilibrium vapor pressure if its surface area is larger. This belief probably arises from our experience that a liquid evaporates faster in the open if it has a larger surface area. The water in a half filled drinking glass may take weeks to completely evaporate, but it will evaporate in a matter of hours if the water is poured on the floor. If the puddle of water is spread out with a mop, it will completely evaporate in a matter of minutes. This is a surface area effect, just as you would expect. A liquid can only evaporate from its surface. Interior molecules are surrounded on all sides by other molecules and can not escape. By increasing the surface area, we allow a greater fraction of the liquid's molecules to be surface molecules. This means more molecules will be leaving the liquid per unit time, so the liquid evaporates faster.
So why doesn't this same phenomenon increase the equilibrium vapor pressure? The difference here is that equilibrium vapor pressure is measured in a closed container, not out in the open. When a liquid evaporates in the open, the condensation rate is negligible. Because of the vast volume surrounding the liquid, a molecule is not likely to return to the liquid once it leaves. Increasing the surface area increases the evaporation rate while having little effect on the condensation rate. The liquid and its vapor do not establish an equilibrium when evaporation takes place in the open. But in a closed container, the gas molecules must remain in the space just above the liquid and are available for condensation. Increasing the surface area still increases the evaporation rate, but that same surface is also available for condensation, so the condensation rate is increased by the same factor. The equilibrium vapor pressure -- which is determined by the balance of these two opposing processes -- is unaffected.
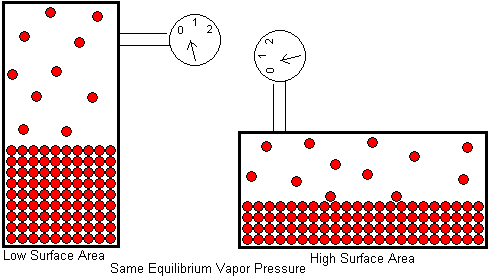
The above drawing shows a liquid in equilibrium with its vapor in a tall container. When the container is laid on its side, the surface area of the liquid is larger, but the equilibrium vapor pressure is unaffected.
Since it is the liquid that is evaporating and generating the gas, there is sometimes a tendency to believe that increasing the amount of liquid in the container will increase the equilibrium vapor pressure. However, liquid can only evaporate from its surface. Adding more liquid to the container just adds more molecules to the bulk liquid. The equilibrium vapor pressure is not affected by the amount of liquid in the container, as long as at least a little liquid is present to be in equilibrium with the gas.
Another misconception that sometimes arises is that the volume
of the container affects the equilibrium vapor pressure. This is only true
if the container is so much larger than the volume of liquid that all the liquid
vaporizes before the equilibrium vapor pressure is reached. But in this
case, we have an all gas system, and the concept of equilibrium vapor pressure
does not apply.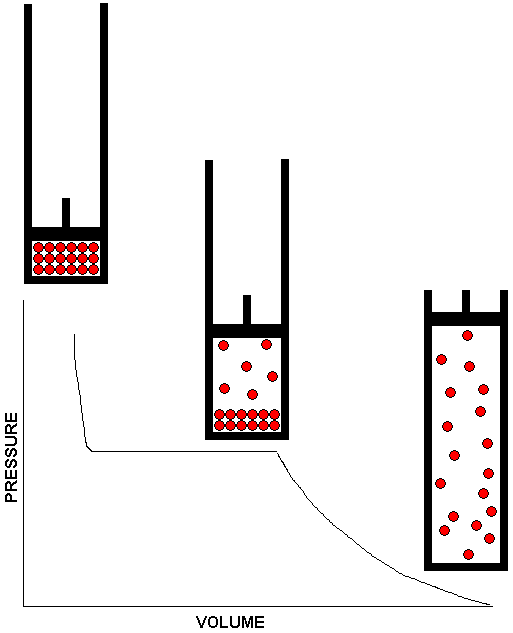
The drawing above shows how a system consisting of a liquid in equilibrium with its vapor responds to changes in volume. The piston and cylinder assembly shown in the middle of the drawing depicts the equilibrium system. There is a volume range -- represented by the plateau on the graph -- over which the system remains in equilibrium at the same vapor pressure. For volumes in this range, lifting the piston causes some of the liquid to vaporize so the larger volume can be filled to the same pressure as the smaller volume. Conversely, if the piston is pushed in to reduce the volume, some of the gas condenses to liquid, thereby removing gas from the system so that the gas pressure in the smaller volume is no larger than it was in the larger volume. The system can only adapt within certain limits, however. If the volume is made too large, all the liquid will vaporize. Once this happens, we no longer have a liquid / vapor equilibrium. After all the liquid has vaporized, any further increase in volume will result in a decrease in pressure. This is shown by the downward curve on the right side of the graph. Also shown is the piston and cylinder assembly containing the all gas system. If the substance under study behaves as an ideal gas, we can use Boyle's Law to calculate the reduction in pressure as the volume is increased. At the other extreme, if the volume is reduced too far, all of the gas will condense to liquid, and the piston will be resting on the surface of the liquid. There is no longer an equilibrium at this point, because the system consists entirely of liquid. Since liquids are essentially incompressible, any further reduction in volume will require an enormous increase in pressure. This is depicted by the steep curve at the left side of the graph. Also shown is the piston and cylinder assembly containing the all liquid system.
We have spent considerable time looking at the vaporization of liquids, and we have also occasionally referred to boiling of liquids. Both of these processes are vaporizations, but boiling is a special kind of vaporization. When water evaporates from an open container at room temperature, evaporation occurs only at the liquid's surface. If you put the water in a pot and boil it on your kitchen stove, vaporization occurs throughout the liquid, not just at the liquid surface. Molecules in the interior of the liquid form gas bubbles. These bubbles, being less dense than the surrounding liquid, will rise to the surface and escape from the liquid. We tend to think of boiling as a temperature phenomenon, when we speak of the boiling points of substances, but boiling is more of a pressure phenomena than a temperature phenomena. A liquid will boil when its equilibrium vapor pressure is equal to the external pressure.

The drawing above shows a gas bubble that has formed in the bulk liquid. Notice that there are interior molecules that have the larger separations that we associate with a gas. A blue circle has been drawn around the bubble to more clearly show the space within which the gas molecules move. Their rapid motion in random directions drives back the liquid molecules and keeps them out of the space occupied by the bubble. Now consider the conditions required for the bubble to exist. The liquid is being heated in an open container, so it is subject to the external atmospheric pressure. If the inward pressure on the bubble (coming from the atmospheric pressure) is larger than the outward pressure exerted by the bubble (determined by the liquid's equilibrium vapor pressure at the existing temperature) the bubble will collapse to a liquid. Therefore, a liquid can not boil if its equilibrium vapor pressure is lower than the external pressure. This is why water normally boils at 100 oC. The equilibrium vapor pressure of water at 100 oC is 760 torr, which is normal atmospheric pressure. At temperatures below 100 oC, the vapor pressure of water will be less than 760 torr, so no bubbles of water vapor can form if the water is in an environment where the pressure is 760 torr. Water can be made to boil at lower temperatures by reducing the pressure on it. At 25 oC, the vapor pressure of water is 23.8 torr. If we reduce the external pressure on the water to 23.8 torr, the water will boil at room temperature! This can be demonstrated by placing a bell jar over a beaker of water and pumping out most of the air with a vacuum pump. Conversely, if we increase the external pressure on water to a value greater than 760 torr, the water will boil at a temperature higher than 100 oC. A pressure cooker takes advantage of this principle to cook foods faster by increasing the temperature of the boiling water. Note that when heating a liquid, it can become no hotter than the boiling point under the existing pressure. Once the liquid begins boiling, adding heat at a faster rate just makes it boil faster at the same temperature. The endothermic vaporization process carries away the added heat.
Liquids can only boil in open containers. In a closed container, the liquid will be subject to the pressure of its own vapor, and this pressure will increase as the liquid temperature increases. No bubbles can form in the liquid because their outward pressure can not exceed the external pressure resulting from the accumulation of gas above the liquid surface. In an open container, the pressure above the liquid remains equal to the applied external pressure. The liquid boils when it reaches a temperature where its vapor exerts the same pressure as the external pressure. If the container is open, you can not build up a higher pressure inside the container than outside of it. This is why the liquid can become no hotter than its boiling point under the existing pressure. To do so would imply a vapor pressure higher than the external pressure. But as we have noted, an open container can not have a higher pressure inside than what exists outside. Since a liquid can not boil in a closed container, perhaps you are wondering what happens if a liquid is intensely heated in a closed container. Assuming the container does not explode, the liquid is eventually converted into a very dense gas, called a supercritical fluid. We will look at this phenomenon in more detail in Section 4.
We have discussed the three states of matter -- solids, liquids, and gases -- and conversions between these states. Which state or states of a substance will be stable depends on the pressure and temperature. A phase diagram is a graph showing the stable state(s) of a substance as a function of pressure and temperature. Pressure is plotted on the Y-axis and temperature on the X-axis. The XY plane is divided into 3 distinct regions -- one for each of the 3 states of matter. There are 3 boundaries where two of the three regions meet. The points on these boundaries correspond to pressures and temperatures at which two states of matter (solid and liquid, solid and gas, or liquid and gas, depending on which boundary) can coexist. The two coexisting states are in equilibrium on the boundaries. There is one point, called the triple point, at which all three boundaries, meet. Because the triple point is a single point, there is only one unique combination of pressure and temperature at which solid, liquid, and gas can all be stable (in equilibrium) at the same time. A typical phase diagram is shown below. The image was taken from General Chemistry, An Integrated Approach, 2nd Edition, By Hill & Petrucci (Prentice Hall, 1999).

On the above graph, point A is the triple point -- that unique combination of pressure and temperature at which solid, liquid, and gas can all coexist in equilibrium. Curve segments AB, AC, and AD are the three boundaries mentioned earlier, each of which separates two states of matter. Curve segment AC is the equilibrium vapor pressure curve for the liquid. As noted in Section 3, equilibrium vapor pressure of a liquid increases with temperature. Similarly, a solid which sublimes has a sublimation pressure, and curve segment AB is nothing more than a plot of the sublimation pressure (i.e., equilibrium vapor pressure) of the solid. Curve segment AD (so steep it is almost a line) separates the solid and liquid regions, and is a plot of pressure and temperature combinations at which solid and liquid can coexist in equilibrium.
Using a phase diagram, we can determine the stable state(s) of a substance at a specified pressure and temperature. To do this, we find the point on the graph that corresponds to the pressure and temperature of interest. If it falls entirely within one region, only the state of matter associated with that region will be stable. If the point falls on a boundary, both of the states which meet at that boundary are stable. If the pressure and temperature of interest correspond to the triple point, all three states of matter are stable.
We can also use phase diagrams to predict what phase changes should occur when a substance is heated or cooled at a particular pressure, or when the pressure on it is increased or decreased at a particular temperature. We locate the point that represents the starting conditions for the substance, and then draw a horizontal line (for heating or cooling at constant pressure) or a vertical line (for increases or decreases in pressure at constant temperature) that leads to the desired ending condition. We can then see which phase boundaries (if any) we have crossed.
In the upper right hand corner of the phase diagram shown above, we see a small gray colored region labeled "SCF". The "SCF" stands for "Super Critical Fluid". This is an interesting region in that it does not have sharp boundaries with the other regions like solids, liquids, and gases do. In terms of what is shown on the graph, we can explain the phenomenon of the super critical fluid as follows:
The vapor pressure curve of the liquid does not continue indefinitely. Rather, it ends abruptly at point C, which is called the critical point. The pressure and temperature corresponding to this point are called the critical pressure and the critical temperature, respectively. At temperatures between the triple point temperature and the critical point temperature, the substance will exist as a gas if the pressure is low and as a liquid if the pressure is high enough. At any given temperature in this range, if we start with the gas at low pressure and gradually increase the pressure, there is a certain pressure at which the liquid state suddenly appears. This pressure corresponds to the equilibrium vapor pressure of the liquid at that temperature. The vapor pressure curve of the liquid (segment AC) serves as a sharp boundary between the gas and liquid states.
Now consider what happens when we compress a gas at temperatures higher than the critical temperature. Because the vapor pressure curve ended abruptly at point C (the critical temperature) and we are working at a temperature hotter than that, we will not have any boundary to cross as we increase the pressure at constant temperature. As we put more and more pressure on the gas, it becomes more and more dense, because its molecules are being squeezed closer and closer together. Eventually, the molecules will be squeezed so close together that the gas is as dense as a liquid. However, at no point did we ever see a liquid form. From this discussion, we see that one way to define the critical temperature is "the temperature above which a gas can not be liquefied solely by the application of pressure". Thus, we can bottle propane (a fuel for camping stoves) as a liquid at room temperature by storing it under pressure, and we can keep butane in liquid form at room temperature when it is stored under pressure in a cigarette lighter. For these gases, room temperature is below the critical temperature, so the gas can be liquefied by pressure alone. But if we need liquid nitrogen (used as a cryogenic liquid in research and industry), we must chill the gas. Pressure alone will not convert gaseous nitrogen to liquid nitrogen because room temperature is above the critical temperature of nitrogen.
In the previous paragraph, we arrived at a supercritical fluid by starting with a gas at a temperature above its critical temperature and compressing it until it had a "liquid-like" density. That is, we reached the supercritical fluid state by changing the pressure as we held the temperature constant. We now consider reaching the supercritical state by adjusting the temperature. We begin with a substance well below its critical temperature, with the liquid and gaseous states in equilibrium in a closed container. We then heat the enclosed substance to a temperature above the critical temperature.
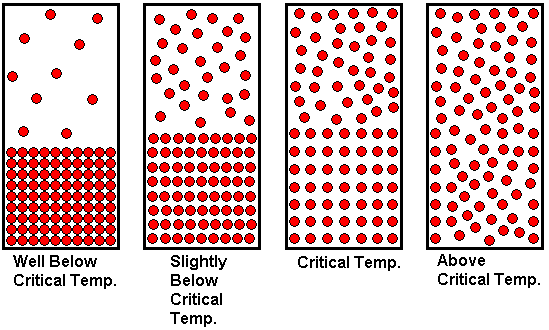
The drawing shown above illustrates how the state of the system changes with temperature. Since equilibrium vapor pressure increases with temperature, we observe that the gas density increases as the system becomes hotter and hotter. A greater number of gas molecules per unit volume increases the gas pressure, because there are more gas molecules to collide with the walls of the container, which is what is responsible for the pressure. At the same time, the liquid expands slightly as it is heated, meaning the density of the liquid decreases as the temperature becomes higher. At lower temperatures, there is a clear distinction between liquid and gas. We can see where the liquid ends and the gas begins. The liquid surface, or interface between liquid and gas is clearly visible because there is a sharp difference in density between liquid and gas. But as the system is heated, the gas density increases while the liquid density decreases. As we approach the critical temperature (from the low temperature side), the two densities become closer and closer together, and the clear distinction between liquid and gas begins to blur. The liquid meniscus disappears at the critical temperature, because the liquid and gas densities have become equal. At this temperature, the two states have merged into one. Above this temperature, only the gas state exists, but the pressure is so high that the gas has a "liquid-like" density. It is still better characterized as a gas than a liquid, because if we allowed the container to expand (i.e., piston and cylinder arrangement) at temperatures above the critical temperature, the substance would expand to uniformly fill the additional volume. This is a characteristic we associate with a gas, not a liquid. Because we refer to it as a supercritical fluid, students sometimes think of it as a liquid, because they have learned to think of "fluid" as another word for "liquid". But remember that fluid just means "having the ability to flow". Gases are fluids too.
You should become familiar with the position of the regions of the phase diagram so you can recognize them even if you are presented with a diagram in which they are not labeled. Their locations are quite logical if you think about it. The solid region is located on the left side of the graph, This means the solid state is stable at low temperatures, relative to liquids and gases. This conforms to common experience -- we must heat solids in order to melt them. Likewise, the position of the liquid state makes sense. At any pressure for which a clear transition from liquid to gas can be made (i.e., any pressure between those of points A and C in the diagram), it requires an increase in temperature to go from the liquid state to the gas state. This again conforms to common experience. We must heat water in order to boil it into steam. The diagram also helps us understand the phenomenon of sublimation. Looking at the phase diagram, we can see that the liquid state does not exist at pressures below the triple point pressure. So if a solid is heated under sufficiently low pressure, it does not melt, but changes directly to a gas -- that is, it sublimes. The triple point pressure for carbon dioxide is 5.1 atm. That is why dry ice (solid CO2) does not melt. We live in a world where the pressure is 1 atm. This is well below the minimum pressure of 5.1 atm required to have liquid CO2. At 1 atm, the solid and gaseous forms of CO2 are in equilibrium at -78 oC. Below this temperature, only the solid state is stable, and above this temperature, only the gaseous state is table. A block of dry ice placed in a room at 25 oC will warm up to -78 oC and will get no warmer. It will maintain that temperature as it sublimes, and it will continue to sublime until all the solid is gone.
In looking at characteristics like equilibrium vapor pressures and normal boiling points, we have noted that they are determined by the strengths of intermolecular attractive forces. All molecules have a least a slight attractive force acting between them when they are close enough together. When molecules are very close together (i.e., in the moment of a molecular collision) they actually repel each other, but the repulsive force is extremely short range. Other than noting that they exist at close range, we will not focus on the repulsive forces. Our concern will be the attractive forces, which act over much longer distances and affect several physical properties.
Chemists have identified three kinds of attractive forces that may act between molecules. One kind of force is a dipole-dipole attractive force. This is a force that is experienced by polar molecules, those that have a non-uniform distribution of electrons because of differences in the extent to which the bonded atoms tend to draw electrons to themselves. For example, consider a hydrogen chloride molecule.
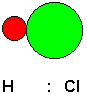
Shown above is a model of the molecule and the Lewis structure emphasizing the unequal sharing of the bonding electron pair (for simplicity, non-bonding electron pairs are not shown). Chlorine has a greater electronegativity than hydrogen, that is, it has a greater tendency to pull shared electron pairs toward itself. This makes the chlorine end of the molecule slightly negative and the hydrogen end slightly positive. These are considered partial charges, because overall, the molecule is neutral, but it has some regions of higher electron density and some regions of lower electron density. If the HCl molecule is brought in the vicinity of another HCl molecule, or for that matter, any other molecule that is also polar, the two molecules will attract each other, just as two magnets will attract each other. Of course, in this case, the attraction involves electric fields rather than magnetic fields, but the effect is similar. We can think of the molecules as little tiny magnets, if this helps us to visualize it.
It is easy enough to understand why polar molecules should attract each other, but not all molecules are polar. For example, consider Cl2.
Since both atoms are chlorine atoms, they have the same electronegativity. Therefore, the Lewis diagram has been drawn with the shared pair placed in the middle between the two atoms. The electron pair does not have a preference for either of the chlorine atoms over the other one.
How can we explain attraction between molecules that are non-polar? The first theoretical explanation of these forces was offered by Fritz London, so these forces are called London forces. The idea is that even though the electrons are uniformly distributed when averaged over time, at any given point, they might not be uniform. Electrons are in constant motion, so if we could take a series of snapshots of the electron distribution we would find that some of the pictures showed a non-uniform electron distribution. It is only when the electron distributions are averaged over a period of time that we obtain a uniform distribution. A polar molecule, on the other hand, has a non-uniform electron distribution even when averaged over time. The polar molecule has a permanent dipole, whereas a non-polar molecule occasionally forms what is called an instantaneous dipole, that is, a temporary non-uniform distribution of electrons. If a molecule with an instantaneous dipole approaches an unpolarized molecule, it will establish an induced dipole in that previously unpolarized molecule. This is similar to the action of a magnet on a paperclip. When the magnet is brought near the paperclip, the paperclip becomes a temporary magnet, polarized in the opposite direction of the approaching magnet. For example, if one end of the paperclip is near the magnet's north pole, that end of paperclip becomes the south pole. Since unlike poles attract, the paperclip is attracted to the magnet.
Generally speaking, the London force is considered to be weak, because the temporary dipoles exist only sporadically, whereas the dipoles in polar molecules remain "on" at all times and provide for continuous attraction. The London forces result in a series of brief tugs tending to pull the affected molecules together. As an aid to visualization, think of the London force as flickering on and off like a fluorescent light about to burn out. Temporary non-uniform electron distributions form and result in an attractive force, but these non-uniform distributions quickly disperse to a more uniform distribution and the attractive force is lost. Soon thereafter, a temporary non-uniform distribution arises again, and the attractive force appears once more.
We tend to think of London forces as weaker than dipole-dipole forces for the reasons noted above, but we must be cautious in this assessment. London forces increase in strength with the size of the molecule, so two large non-polar molecules may have stronger attractive forces than two small polar molecules. There are more electrons present in larger molecules than in smaller molecules, and the larger the number of electrons, the greater the volume over which they "spread out". That is, the electron cloud is more diffuse in larger molecules, and diffuse electron clouds are more easily polarized (made non-uniform). What we can say, then, is if we compare two molecules of about the same size, we expect the polar molecule to have stronger attractive forces than the non-polar molecule. For the sake of this comparison, we assume neither of the molecules in question can form hydrogen bonds, which is another kind of attractive force we must consider. Before going on to consider hydrogen bonding, however, there is one more attribute of the London force we should consider. In addition to depending on the molecule's size, it also depends to some extent on the molecule's shape. If we compare two molecules of the same molecular weight, the molecule with the more elongated shape tends to have stronger London forces. There is more molecular surface area over which the London forces can act in an elongated molecule as compared to a more compact molecule.
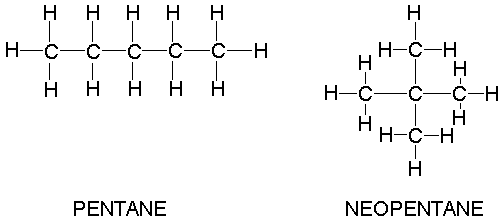
For example, we expect stronger London forces in liquid pentane than in liquid neopentane. This is consistent with the observed boiling points of these substances. The normal boiling point of pentane is 36.1 oC, while that of neopentane is 9.5 oC. Higher boiling points mean that more energy is needed to separate the liquid molecules to make them gas molecules. This in turn means the attractive forces must be stronger. It is common practice to gauge the strength of intermolecular attractive forces in liquids by comparing their boiling points.
Hydrogen bonding is an especially strong attractive force that can exist between two molecules only if they meet these two requirements:
One of the molecules contains a hydrogen atom covalently bonded to an atom of fluorine, oxygen, or nitrogen.
The other molecule contains an atom of fluorine, oxygen, or nitrogen. It need not have hydrogen covalently bonded to it, but it may.
A molecule which meets the requirements of item 1 above is able to establish hydrogen bonds to a molecule capable of receiving them. A molecule that meets the requirements of item 2 may receive hydrogen bonds from a molecule that is capable of establishing them. Notice that any molecule that meets the requirements of item 1 automatically meets the requirements of item 2. The molecule in item 1 uses the H atom that is covalently bonded to F, O, or N to establish a hydrogen bond with another molecule, but it could also receive a hydrogen bond using that same F, O or N atom. This means any molecule capable of establishing hydrogen bonds is also capable of receiving them. For example, an H2O molecule can hydrogen bond with another H2O molecule, and with an NF3 molecule, but two NF3 molecules can not hydrogen bond with each other since neither molecule contains hydrogen. Two CH4 molecules can not hydrogen bond with each other because there is no F, O, or N present.
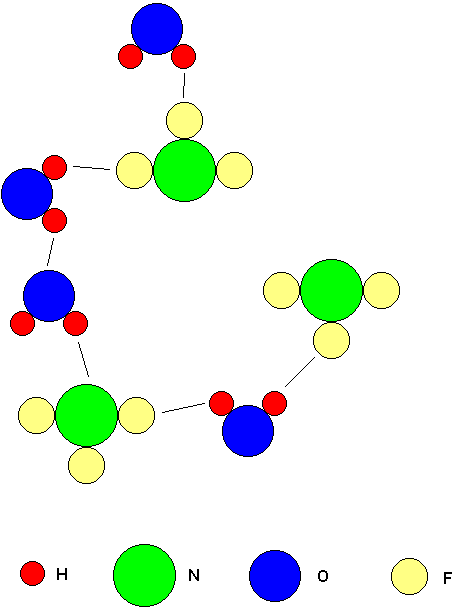
The above drawing shows molecules of H2O and NF3. The black lines extending between molecules indicate the hydrogen bonds. Notice that H2O can establish hydrogen bonds with other H2O molecules and with NF3 molecules. An H2O molecule meets the requirements of both item 1 and item 2, so it can serve as an establisher or receiver of hydrogen bonds. An NF3 molecule meets the requirements of item 2 but not item 1. Therefore, an NF3 can only receive hydrogen bonds from other molecules capable of establishing them. An NF3 molecule can not establish any hydrogen bonds of its own. As a result, it is not possible for two NF3 molecules to hydrogen bond each other.
What is so special about the elements nitrogen, oxygen and fluorine that only these can make hydrogen bonding possible? These are the three most electronegative elements in the periodic table. When a hydrogen is covalently bonded to one of them, the shared electron pair is considerably shifted away from hydrogen and toward the other, more electronegative element. Because the hydrogen atom has no core electrons, the nucleus is left somewhat exposed by the unequal sharing of the bonding pair. The high charge density of the hydrogen nucleus attracts some of the electron density around a sufficiently electronegative atom. The interaction is strong enough to give it a special name -- the hydrogen bond. Only nitrogen, oxygen and fluorine are electronegative enough to significantly participate in hydrogen bonding. The strength of the hydrogen bond is sufficient to give special properties to substances in which hydrogen bonding occurs. For example, the boiling point of water is quite high for a substance of its molecular weight. Most substances with molecular weights close to that of water (18 g/mol) are gases at room temperature (25 oC), but the normal boiling point of water is 100 oC. The unusually high boiling point of water is attributed to the necessity of breaking hydrogen bonds in order to separate H2O molecules from each other in the liquid state in order to make them gas molecules.
Hydrogen bonding is generally considered to be the strongest of the three intermolecular attractive forces. From our earlier discussion comparing the dipole-dipole force and the London force, we now have the following ranking in order of increasing strength:
(weakest) London force < dipole-dipole force < hydrogen bonding (strongest)
But again, we have to make this statement with caution because the London force can vary considerably with the size and shape of the molecule. We must also remember that the London force can exist between any two molecules, regardless of their chemical composition. That's because the London force results from an instantaneous non-uniformity of electrons that happens by chance. Since all molecules have electrons, any molecule is a candidate for this kind of force. This means that in molecules that have dipole-dipole forces and / or hydrogen bonding, the London force is still present and is in addition to those other forces.
There are several properties of liquids that are affected by the strength of the intermolecular attractive forces. We shall briefly look at some of these properties.
Normal boiling point: As we have noted, the stronger the intermolecular attractive forces, the higher the normal boiling point will be. Stronger forces require more energy (supplied as heat, hence the higher temperature) in order to overcome them and change the liquid into a gas.
Equilibrium vapor pressure: At any given temperature, the stronger the attractive forces, the lower the equilibrium vapor pressure. If the forces are stronger, fewer molecules will have enough energy to escape from the liquid surface and become gas molecules. If there are fewer molecules in the gas phase, there will not be as many collisions of gas molecules with the container walls. This means the gas pressure will be lower.
Heat of Vaporization: Energy must be put into the system in order to vaporize a liquid. The attractive forces holding the molecules in the liquid must be overcome, and this is an endothermic process. The stronger the attractive forces are, the more energy that must be supplied to overcome the forces, and therefore, the more endothermic the vaporization process will be. Comparing two substances at the same temperature, the substance with stronger attractive forces is expected to have a larger heat of vaporization (DHvap). For any given substance, the heat of vaporization decreases slightly as the temperature increases. This is because at higher temperatures, the increased thermal energy of the molecules has already partially overcome the attractive forces, so there is less "work" remaining to be done. For example, water has the following heats of vaporization:
H2O(l) ----------> H2O(g) ΔHvap = 44.0 kJ at 25 oC
H2O(l) ----------> H2O(g) ΔHvap = 40.7 kJ at 100 oC
Viscosity: The resistance of a liquid to flow is called viscosity. You know that syrup pours more slowly than water. We say that syrup is more viscous than water, or worded another way, syrup has a higher viscosity than water. In order for a liquid to flow, its molecules must move relative to each other. The stronger the intermolecular attractive forces, the more difficult this will be. Therefore, we expect stronger intermolecular attractive forces to increase the viscosity of a liquid. The viscosity is also temperature dependent. At higher temperatures, the attractive forces are "weakened" by the higher thermal energy of the molecules. This makes it easier for the molecules to move past each other. A liquid is expected to have a lower viscosity when hot.
Surface Tension: This is the phenomenon that allows you to slightly overfill a glass of water without the water spilling over the sides of the glass. It is also the phenomenon that allows small insects to walk on the surface of a lake. Surface tension is caused by an imbalance in attractive forces experienced by molecules at the liquid's surface. Molecules in the interior of the liquid are surrounded on all sides by other molecules and experience a force that is equal in all directions. But molecules on the surface of the liquid have no liquid molecules above them, so they experience attractive forces from the sides and from below, but not from above. This makes the surface molecules jam together somewhat, and makes the liquid surface act as if it has a "skin". The stronger the attractive forces, the greater the imbalance in those forces at the liquid's surface. Therefore, we expect surface tension to be higher in a liquid with strong attractive forces than in a liquid with weak attractive forces. For a given liquid, the surface tension decreases as the temperature increases. At higher temperatures, some of the attractive forces are disrupted by the increased thermal energy of the molecules. That is, the forces are somewhat "weakened" at higher temperatures, making them easier to overcome.