When we first learned about the equilibrium constant
expression, we did not consider the physical states of the reactants and
products. We took the generic
equation
aA +
bB <---------->
cC +
dD
(1)
and derived the equilibrium constant expression
[C]eqc[D]eqd
KC =
---------------
(2)
[A]eqa[B]eqb
In our earlier consideration of equilibrium, the only
significance we put on the physical state of the substances in the equation was
that if they were gases, we could consider an equilibrium constant that is
defined in terms of gas pressures instead of molar concentrations.
For example, taking substances A, B, C and D to all be gases,
aA(g) + bB(g) <----------> cC(g) + dD(g) (3)
we can write the pressure-based equilibrium constant
PC eqc
PD eqd
KP =
----------------
(4)
PA eqa PB eqb
In deriving KC (and similar arguments would hold
in a derivation of KP) the idea was that constants were gathered on
the left side of the equation and quantities that could vary were gathered on
the right side of the equation. Recall
that the concentration-based equilibrium constant KC was just the
ratio of the forward rate constant to the reverse rate constant:
kf
KC =
---
(5)
kr
The forward and reverse rate constants are independent of
concentration, so KC≠ is likewise independent of concentration.
In equation (2), the individual concentrations can vary from one
equilibrium mixture to the next, but the mathematical result of substituting all
of those concentrations into the expression is always the same number.
But some concentrations never vary, so it makes sense to
just absorb those constant concentrations into the equilibrium constant, and
include on the right hand side of the equation, only those concentrations that
can truly vary. We will see that
when a substance is a gas or is dissolved in water (or any other solvent for
that matter Ė but water is the most common) its concentration can vary, but
when it is a liquid or a solid, its concentration can not vary.

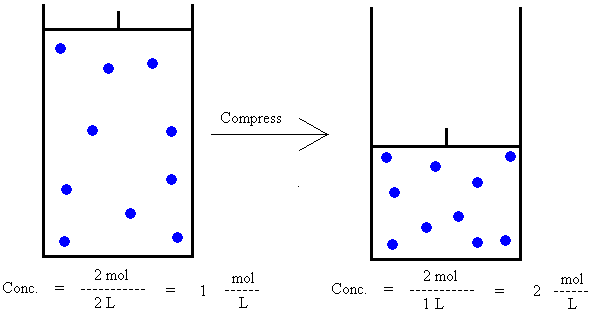
Figure 1.
If 2 moles of gas occupies a volume of 2 liters,
then the concentration is 2 mol / 2 L = 1 mol/L.
If the 2 moles of gas is then compressed to
occupy a volume of 1 liter, 2 mol / 1 L = 2 mol/L.
Now consider the aqueous
(dissolved in water) state. You
know from experience that substances in solution can have a variable
concentration. If you put sugar in
your tea or coffee, you can adjust the sweetness to your personal taste by
choosing the amount of sugar you dissolve.
Two teaspoons of sugar in a glass of tea makes a sweeter drink than only
one teaspoon.
Unlike gases and substances in solution, liquids and solids have an essentially constant concentration. This is because liquids and solids are practically incompressible. The molecules in liquids and solids are very close together, with very little room to squeeze any closer. As a result, it takes an enormous pressure to cause even a tiny reduction in volume. In most circumstances, we can ignore any changes in volume for a solid or liquid substance.
Consider water as an example.
Perhaps you have learned in one of your science classes that the density
of water is 1.00 g/mL. Will this
value ever change? Well, to a tiny
extent, yes. But normally not
enough to worry about. Temperature
will have a small effect, because water will expand when heated and contract
when cooled. Since density is mass
divided by volume, changing the volume occupied by any given mass of water will
change its density. But the volume
changes are very small. If you put
some water in a pot on your stove and heat it all the way from room temperature
to boiling, you donít notice any obvious increase in the waterís volume.
And because water (like other liquids and solids) is nearly
incompressible, ordinary atmospheric pressure changes are not going to affect
the volume of a water sample. Working
to 3 significant figures, we can safely say that water is always 1.00 g/mL.
And if water always has this density, then it always has the same molar
concentration. In fact, we can
calculate the molar concentration of any substance from its density. Here is the calculation for water:
g
1000 mL
1 mol
mol
1.00 ------- x
------------- x ------------
= 55.5
--------
mL
1 L
18.02 g
L
The only way water can have a
concentration other than 55.5 mol/L is if it has a density other than 1.00 g/mL.
So if we donít have to consider any changes in density, then we donít
have to consider any changes in molar concentration either.
Now lets revisit the generic
equilibrium reaction in equation 1, but this time lets assign some particular
physical states to the substances in that equation.
aA(s) + bB(aq) <----------> cC(g) + dD(aq) (6)
Up until now, these physical
states would not make any difference to us, and we would still write the
concentration-based equilibrium constant (KC) as
[C]eqc[D]eqd
KCí =
--------------
(7)
[A]eqa[B]eqb
just as before.
The only difference between equation 7 and equation 2 is that I have
added a prime mark to KC to
make it temporarily look different. You
will see momentarily why I chose to do this.
We now make the following
argument: Substance A is a solid, so its concentration is essentially constant.
Therefore, it belongs on the left side of the equation with the constant,
rather than the right side, with the things that can vary.
If we multiply both sides of equation 7 by [A]eqa
we get
[C]eqc[D]eqd
KCí . [A]eqa
= ----------------
(8)
[B]eqb
When the right side of equation 7 is multiplied by [A]eqa, it cancels out, therefore this concentration does not appear on the right side of equation 8. Notice that the left side of equation 8 contains two constants: KCí and [A]eqa. Since a constant multiplied by a constant is just another constant, we can declare KC (without the prime mark) to be equal to the product of KCí and [A]eqa. That is,
KC
= KCí
. [A]eqa
(9)
Substituting equation 9 in
equation 8 gives
[C]eqc[D]eqd
KC =
-----------------
(10)
[B]eqb
Notice that the only difference between the right hand side of equation 10 and the right hand side of equation 2 is that the concentration of substance A is missing. This is precisely the one substance which was a solid. All the other substances were said to be either aqueous or gaseous. Of course, equation 10 was derived on the basis of substance A being the one and only substance to have a constant concentration. A different equation would result if a different substance (or substances) in the equation were considered to have a constant concentration. But we donít need to re-derive an equation like equation 10 every time we change which substances have a constant concentration. In every case, the only difference between such an equation and equation 2 is that the substances with a constant concentration are omitted from the right hand side of the equation. Their constant concentration is considered to be ďabsorbed in the equilibrium constantĒ.
So the new rule we will now
always apply is:
Write concentration-based equilibrium constant expressions in the mathematical form you have learned about in the very beginning of your study of equilibrium, except omit those substances that are solid or liquid. Include only substances in the aqueous or gaseous state in your concentration-based equilibrium constant (KC).
The above discussion has focused mainly on concentration-based (KC) equilibrium constants. Equations 3 and 4 did consider pressure-based (KP) equilibrium constants, but in those equations, all the substances were assumed to be gases. Perhaps you were wondering how you would handle KP if only some of the substances were gases, but not all of them were. The answer is that those substances that are in aqueous solution would continue to be included in the equilibrium constant expression as molar concentrations, with only the gases being entered as pressures in atmospheres. Although we must enter the concentrations as moles per liter or atmospheres as appropriate, we normally donít enter the units. Thatís because thermodynamic equilibrium constants are dimensionless numbers. We should actually be using something called activities rather than concentrations in moles per liters and pressures in atmospheres, but the use of moles per liter and atmospheres gives Ė at least for our purposes Ė a good approximation of the thermodynamic equilibrium constant. And speaking of activities:
In equations 6 through 10, you saw how the constant concentration of a solid (and the same argument would hold for a liquid) can be used to exclude it from the equilibrium constant expression. Hereís an even better explanation for why solids and liquids are excluded: pure solids and liquids have an activity of 1. Activities are dimensionless numbers, so a pure solid or liquid does not change the value of an equilibrium constant. Neither multiplying nor dividing by 1 changes anything. Thatís the real reason solids and liquids donít appear in equilibrium constant expressions. However, the explanation put forth in the development of equations 6 through 10 makes more sense to students who are accustomed to thinking in terms of molar concentrations rather than activities.
For the reaction in equation 6
aA(s) + bB(aq)
<----------> cC(g)
+ dD(aq)
(6)
the pressure-based (KP)
equilibrium constant expression is
PC eqc
[D]eqd
KP =
------------------
(11)
[B]eqb
Only substance C is entered as a pressure, because only
substance C is a gas. Substances B
and D are in aqueous solution, and they continue to appear as molar
concentrations. Substance A does
not appear, because it is a solid.
To summarize, then, solids and liquid are omitted from both the concentration-based (KC≠) and pressure-based (KP) equilibrium constant expressions. In concentration-based (KC) equilibrium constant expressions, both aqueous and gaseous substances appear as molar concentrations. In pressure-based (KP) equilibrium constant expressions, gaseous substances appear as pressures, and aqueous substances continue to appear as molar concentrations.