We are all familiar with solutions from activities in our daily lives. Everyone knows that salt and sugar are soluble in water. We dissolve sugar in water when we sweeten our coffee or tea, and we dissolve salt in water when following a recipe that calls for salt. Chemically speaking, we can define a solution as a homogeneous mixture of two or more substances. The term homogenous means that the mixture has a uniform composition. Consider a glass of sugar-water, for example. You can take a spoonful of the solution from the top of the glass and taste it to determine its sweetness, or you can use a soda straw to withdraw the liquid from the bottom of the glass rather than the top. In either case, you will taste the same level of sweetness. The concentration of sugar -- that is, the ratio of sugar to water -- is the same in all parts of the glass. On the other hand, if you mix some beach sand in with the sugar in your sugar bowl, you will find that the relative amounts of sugar and sand are not the same in all parts of the sugar bowl. In some spoonfuls, you will draw out more sugar, while other spoonfuls you will draw out more sand. This is a hetergeneous mixture, that is, a mixture that does not have a uniform composition. Such mixtures are not solutions, Solutions are always homogeneous.
When we prepare solutions, we generally have considerable control over the relative amounts the the substances making up the solution. For example, when we make ourselves a glass of tea, we can choose the number of teaspoons of sugar we will dissolve in the tea. Some people like their tea sweeter than others. For the chemist, this means there must be a way of expressing the concentration of the solution -- the relative amount of one substance as compared to another substance or to the total amount of solution. There are many different ways of expressing concentration and we shall look at several of them, learning not only their meaning but also how to convert from one concentration unit to another. We will also look at the physical properties of solutions, and why solutions form in some cases but not in others.
Although a solution could contain hundreds of individual chemical substances, the ones we most commonly look at in general chemistry contain only two components. We designate one of these as the solvent and the other as the solute. While it may be a rather imprecise definition, I think everyone will understand the meaning of these terms if I define the solvent as the substance that "does the dissolving" and the solute as the substance that "gets dissolved". When we mix sugar and water, it is only natural to think of the water as dissolving the sugar. We don't think of the sugar as dissolving the water. Therefore, water is the solvent and sugar is the solute. The solvent determines the state (solid, liquid or gas) of the solution and is generally the component present in greater amount. Thus water, as a liquid solvent, makes liquid solutions, such as sugar-water. Solutions are most often encountered as liquids, but not all solutions are in the liquid state. Air, a mixture of several gases, can be thought of as a solution of these gases in nitrogen (that is, with nitrogen as the solvent) because the nitrogen is far more abundant than any other gas in the mixture. Most solid solutions we encounter are metal alloys. For example, brass is a solid solution consisting of zinc (solute) dissolved in copper (solvent) and solder (an alloy used for connecting components in electronic circuits) consists of lead (solute) dissolved in tin (solute).
In the Introduction section of these notes, it was mentioned that sugar and salt will dissolve in water. These are two examples of cases where a solution will form, but there are also plenty of examples where a solution will not form. We have all heard the phrase "oil and water don't mix". There are two factors that influence solution formation: entropy and enthalpy. These are considered in the following two sections.
Entropy is the thermodynamic function which quantifies the degree of disorder, or randomness in a chemical system. Since nature seems to tend toward a state of maximum disorder, those process which increase the disorder of a system might be expected to occur quite readily, and many do so. When a solute and solvent mix to form a solution, entropy is usually increased.

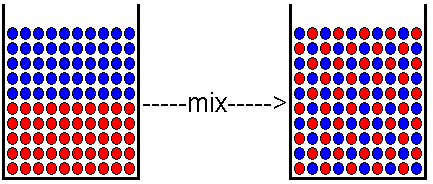
Figure 1. When a solute (shown in blue), dissolves in a solvent (shown in red), the entropy of the system is usually increased. Before mixing, all the solute molecules are gathered in one place, and all the solvent molecules are likewise gathered in one place. This segregation of molecules by type represents a kind of order. When the molecules are mixed so that solute molecules are dispersed among the solvent molecules, there is more randomness, and therefore, a higher entropy or disorder. This is a general argument that applies in most but not all cases. There are some situations -- such as dissolving certain ionic compounds in water -- in which the water molecules become more ordered when they surround the ions. In those cases, formation of the solution can result in a more ordered system. The illustration above assumes simple mixing of the molecules and an increase in the entropy of the system.
Enthalpy is not a new concept to you. Do you remember the topic of "Thermochemistry" from General Chemistry I? We spent a fair amount of time learning how to calculate DH for chemical reactions. The symbol H represented the enthalpy, so DH was the change in enthalpy that accompanied a chemical reaction. Recall that we were able to think of enthalpy as "stored up energy", so that when a chemical reaction resulted in a decrease in enthalpy, heat was given off and when it resulted in an increase in enthalpy, heat was absorbed.
In the previous section, we considered the change in entropy that accompanied the formation of a solution (Figure 1) and we saw that the entropy of the system usually increases in such a process. Now we must consider the change in enthalpy that accompanies the solution formation process.
Depending on the substances involved, the enthalpy may increase, decrease, or stay the same. Nature tends to favor lower energies over higher ones. Your car can coast down a hill in neutral, but it can't coast back up the hill. The gravitational potential energy is lower at the bottom of the hill, so when allowed to move without the assistance of the engine, your car naturally seeks the lowest available position in the gravitational field.
Applying this concept to chemistry, it means that exothermic processes -- those in which enthalpy is decreased -- tend to be favored. So if two substances have an exothermic mixing process, they will probably be quite soluble in each other. Assuming the entropy change is positive, we will have both factors -- entropy and enthalpy -- favoring solution formation. Thus, the solution will readily form. If the mixing process does not result in a change in enthalpy, then the process -- from an enthalpy standpoint -- is neither favored nor disfavored. The two substances involved in such a process will still be soluble in each other if the mixing process increases the entropy (usually the case).
Now consider two substances for which the mixing process is endothermic. If the mixing process increases the entropy (as it usually does), then the changes in entropy and enthalpy work against each other. Dissolving one substance in the other increases the entropy (favorable) but it also increases the enthalpy (unfavorable). The extent to which the two substances will dissolve in each other depends on the balance of these two opposing characteristics. If the solution process is only slightly endothermic, the substances may be soluble in each other to some extent, though the endothermicity of the process will probably limit the solubility. In this case, the increase in entropy outweighs the increase in enthalpy, giving the substances some solubility in one another, even if limited. Now consider two substances for which the mixing process would be extremely endothermic. In this case, the increase in enthalpy that would accompany mixing is so large that it offsets the favorability of increasing the entropy and the two substances are insoluble in each other.
When one substance dissolves in another, the enthalpy change for the process is determined by the strengths of the intermolecular attractive forces that exist between the molecules. Although the dissolving process occurs "all at once", we can split it on paper into three hypothetical steps.
Step 1: Separate the solvent molecules to make room for the solute molecules.
Step 2: Separate the solute molecules to make room for the solvent molecules.
Step 3: Bring all the molecules together so that the solute and solvent molecules are mixed.
Any two molecules that are close enough together will have at least a small attractive force acting between them. The strength of the attractive force will depend on the identities of the molecules, but at least some force will be present unless the molecules are too far apart. In order to separate molecules that are attracting each other, energy must be put in to the system -- it takes effort to pull things apart that are trying to stick together. That is, the separation of molecules mentioned in Step 1 and Step 2 above are endothermic processes. However, in Step 3, we allow molecules to come together. When things that are attracted to each other are allowed to come together, energy is released -- that is, the process is exothermic. So in the above 3-step process, Steps 1 and 2 are endothermic and Step 3 is exothermic. If we add the DH's of the three steps, we get the DH of the overall process. That is,
DHsolution = DH1 + DH2 + DH3 (Eq. 1)
Depending on the relative magnitudes of DH1, DH2, and DH3, DHsolution could be positive, negative, or zero. The case where DHsolution = 0 is rare. Two substances which dissolve in each other without a change in enthalpy are said to form an ideal solution. An ideal solution is one in which the attractive force is the same between all molecules, regardless of their chemical identity. There is probably no truly ideal solution, just as there is no truly ideal gas. There are, however, some solutions that come close to being ideal. Two substances with very similar molecules will come close to forming an ideal solution. If the molecules are similar, they probably have similar attractive forces. Thus, the criterion of equal attractive forces is more likely to be met. Benzene (C6H6) and toluene (C7H8) provide an example of two substances which come close to forming an ideal solution. Do not confuse the characteristics of an ideal solution with those of an ideal gas. An ideal gas has no attractive forces between its molecules, whereas an ideal solution can have attractive forces between the molecules, but they are all equal in strength regardless of the chemical identity of the molecules.
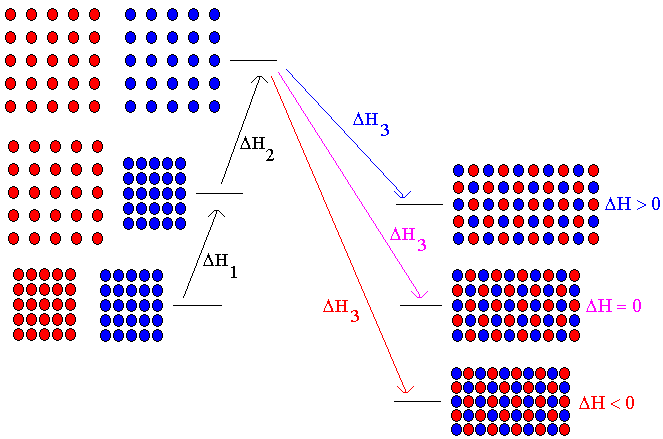
Figure 2. Enthalpy changes accompanying solution formation. Starting with the pure solvent and solute, we separate the solvent molecules. This is Step 1, an endothermic process having an enthalpy change of DH1. Next, we separate the solute molecules. This is Step 2, an endothermic process having an enthalpy change of DH2. Finally, we allow the separated molecules to come back together to form the solution. This is Step 3, an exothermic process having an enthalpy change of DH3. The diagram shows three possible situations for the thermodynamics of solution formation. Case 1: If the solvent and solute molecules attract each other more weakly than they attract their own kind, less energy will be released when they are brought together (DH3) than what was required to separate the molecules (DH1+DH2). Overall, the solution formation process will be endothermic. The volume of the solution will be greater than the pure components because the molecules do not attract each other as well in the solution as when they were unmixed. Case 2: If the attractive force is the same between all molecules, the amount of energy released when the solvent and solute molecules come together (DH3) will be the same as the amount of energy needed to separate these molecules from their own kinds (DH1+DH2). Overall, the solution formation process will be neither endothermic nor exothermic. The volume of the solution will be equal to the volume of the pure components, because the molecules in the solution attract each other to the same extent that they attracted their own kinds. This is an ideal solution. Case 3: If the solvent and solute molecules attract each other more strongly than they attract their own kind, more energy will be released when they are brought together (DH3) than what was required to separate the molecules (DH1+DH2). Overall, the solution formation process will be exothermic. The volume of the solution will be less than the pure components because the molecules in the solution attract each other more strongly and pull closer together.
Several different units of concentration are used by chemists. The choice of units to use is often suggested by the phenomena being studied. We will see in later sections of these notes that certain calculations are best performed with the concentration expressed in a particular unit. The units we will consider in some detail here are:
Molarity (abbreviation: M)
Molality (abbreviation: m)
Mole Fraction (abbreviation: X)
Mass Percent of Solute
Molarity is defined as the number of moles of solute per liter of solution, that is
# of moles of solute
Molarity =
--------------------
(Eq. 2)
# of liters of solution
Note that the volume used is the volume of the solution, not the volume of solvent used to prepare the solution. To prepare a 1 M (that is, 1 molar) solution of NaCl in water, you could measure out 1 mole (58.44 g) of NaCl, add this to a volume of water that is considerably less than one liter, stir to dissolve the NaCl, and then add water to bring the total volume up to one liter. If you started with a liter of water and added one mole of NaCl to it, the solution concentration would be less than 1 M, because the solution volume would be greater than one liter. The NaCl being added to the water would increase the liquid volume above its starting value of 1 L.
Molality is defined as the number of moles of solute per kilogram of solvent, that is,
# of moles of solute
Molality =
----------------------- (Eq. 3)
# of kg of solvent
Notice that this concentration unit is defined in terms of the mass of the solvent, not the mass of the solution. To prepare a 1 m (that is, 1 molal) solution of NaCl in water, you could measure out 1 kg (that is, 1000 g) of water and dissolve 1 mole (58.44 g) of NaCl in that 1 kg of water. One advantage molality has over molarity is that it is a temperature independent unit. There is a specified number of moles of solute per kg of solvent, and this ratio will not change as the solution is heated or cooled. Since the volume of an aqueous solution will change slightly with temperature, so will the molarity. For example, if you prepare a 1 L solution of NaCl having a concentration of 1 M (as described in Section 3.1) at 20 oC and then warm the solution to 25 oC, the solution will expand slightly so that it occupies slightly more than 1 L. Since the number of moles of NaCl (1 mole in this case) has not changed, the concentration will now be slightly less than 1 M.
Mole fraction is a convenient unit for calculating equilibrium vapor pressures of solutions, and for expressing concentrations in complicated mixtures, in which there are multiple solutes, or in which we can't make a clear distinction between solute and solvent. You can express the concentration of any substance in a mixture as a mole fraction. The mole fraction is a dimensionless number obtained by dividing the number of moles of the substance of interest by the total number of moles of all substances in the solution. That is,
ni
Xi =
-------------
(Eq, 4)
n1
+ . . . nk
In Equation 4, the variable n stands for the number of moles of a substance, and the n is subscripted with a label to indicate which substance. The substance of interest has been designated "substance i", so the variable n in the numerator carries a subscript of i. In the denominator, we have to add up the moles of all the substances that are present in the solution. In Equation 4 above, the label k has been used to represent the number of substances in the solution. Therefore, we must add up n1 (the number of moles of "substance 1") through nk (the number of moles of substance k). If we have a two component solution (one solvent and one solute) the k is equal to 2. In such a case, however, we could use "solute" and "solvent" as labels rather than "1" and "2". With this in mind, the mole fraction of a solute in in two-component solution can be written as
nsolute
Xsolute =
---------------------- (Eq. 5)
nsolute + nsolvent
In some cases (for example, calculating the vapor pressure of a solution), we will need the mole fraction of the solvent. The equation for this (in a simple two-component solution) can be be obtained by changing the labels slightly in Equation 5.
nsolvent
Xsolvent =
---------------------- (Eq. 6)
nsolute + nsolvent
When the mole fractions of all substances in the mixture are added together, the result is always 1. This is similar to the way percentages must always add up to 100%. That is,
X1 + . . . + Xk = 1 (Eq. 7)
In Equation 7, there are a total of k substances in the mixture, and sum is taken over all k substances. In a simple two-component solution, we can write
Xsolute + Xsolvent = 1 (Eq. 8)
Notice that in a two-component system, if you know the mole fraction of either the solute or solvent, you automatically know the other as well, because they must add up to 1. The mole fractions can not vary independently in a two-component system.
The largest mole fraction a substance can have is 1, which occurs when you have the pure substance. In a sample of distilled water (pure water), the mole fraction of H2O is 1. If two or more substances are present, every substance must have a mole fraction less than 1, and the sum of all of them must be 1.
The mass percent of solute tells what percent of the solution's total mass is due to the presence of solute. You can think of it as the number of grams of solute in a 100 g solution. For example, if you dissolve 5.00 g of sugar in 95.00 g of water (therefore giving 100.00 g of solution), you have a 5.00% sugar solution. In a 100 g sample of the solution, you have 5.00 g of sugar. Even if you don't have 100 g of the solution, the percentage will still be 5.00 %. For example, if you take only 50.00 g of the solution prepared as described above, you will have 2.50 g of sugar dissolved in that amount of solution. The number 2.50 is 5.00 % of 50.00. We can write the following equation for this concentration unit:
mass of solute
Mass% solute = 100% x
-------------------
(Eq. 9)
mass of solution
In a two-component solution, the mass of the solution is the sum of the masses of the solute and solvent, that is
mass of solution = mass of solute + mass of solvent (Eq. 10)
Equation 10 can be substituted into Equation 9 to obtain the following:
mass of solute
Mass% solute = 100% x
--------------------------------------- (Eq.
11)
mass of solute + mass of solvent
In Equations 9 and 11, the quantity 100% should be as interpreted as the number 100 with units of %, not the quantity "1". We multiply by 100 when evaluating these equations.
There are two general types of calculation we will encounter:
Calculating a solution concentration in a particular unit
Converting a concentration from one unit to another
Example 1: What is the molarity of a solution that is prepared by dissolving 0.178 moles of NaCl in enough water to make 455 mL of solution?
0.178 mol
Molarity = --------------- = 0.391 M
0.455 L
Notice that the volume had to be expressed in liters, and that we can abbreviate mol/L as M.
Example 2: What is the molarity of a solution prepared by dissolving 25.7 g NaCl in enough water to make 153 mL of solution?
1 mol
25.7 g x -----------------
= 0.4398 mol
58.44 g
0.4398 mol
Molarity = ----------------- =
2.87 M
0.153 L
Notice that the mass of NaCl has to be converted to moles, and the volume of the solution had to be expressed in liters. The data given in the problem limited our precision to 3 significant figures. The number of moles was carried out to 4 figures and the final answer was rounded off to 3 significant figures. Recall from General Chemistry I that it is best to carry extra figures in your intermediate answers and wait until the final answer is obtained to round off to the correct number of significant figures. The answer comes out in units of mol/L, which is abbreviated M.
Example 3: What is the molality of a solution prepared by dissolving 0.785 moles of KI in 895 g of water?
0.785 mol
molality = ----------------
= 0.877 m
0.895 kg
Notice that the mass of the solvent had to be expressed in kilograms (kg). The answer comes out in units of mol/kg, which can be abbreviated m.
Example 4: What is the molality of a solution prepared by dissolving 25.4 g KI in 963 g of water?
1 mol
25.4 g x -----------
= 0.1530 mol
166.0 g
0.1530 mol
molality = ---------------
= 0.159 m
0.963 kg
Notice that the mass of KI had to be converted to moles, and the mass of solvent (water) had to be expressed in kg. The answer is in units of mol/kg, which can be abbreviated as m.
Example 5: What is the mole fraction of NaCl in a solution prepared by dissolving 1.54 moles of NaCl in 9.73 moles of water?
nNaCl
1.54
mol
1.54 mol
XNaCl = -----------------
= ------------------------- =
--------------- = 0.137
nNaCl + nH2O
1.54 mol + 9.73
mol 11.27 mol
Notice that mole fraction has no units, because the mol unit cancels out.
Example 6: What is the mole fraction of NaCl in a solution prepared by dissolving 15.11 g NaCl in 275.2 g H2O?
1 mol
15.11 g x -----------
= 0.25856
mol (for NaCl)
58.44 g
1 mol
275.2 g x -----------
= 15.272
mol (for H2O)
18.02 g
nNaCl
0.25856
mol
0.25856 mol
XNaCl = -----------------
= --------------------------------- =
--------------- = 0.01665
nNaCl + nH2O
0.25856 mol + 15.272
mol
15.531 mol
Notice that both masses (solute NaCl and solvent H2O) had to be converted to moles. Mole fraction is dimensionless because the mol unit cancels out.
Example 7: What is the mass percentage of sucrose, C12H22O11 in a solution prepared by dissolving 5.17 g of sucrose in 89.74 g of water?
mass of solution = mass of solute + mass of solvent
= 5.17 g + 89.74 g
= 94.91 g
mass of
solute
5.17 g
Mass% solute = 100% x
------------------- = 100%
x --------- =
5.45%
mass of
solution
94.91 g
Notice that the solute mass is expressed as a percentage of the solution mass, not the solvent mass. In the above calculation, the solute and solvent masses were added to produce the solution mass, which was 94.91 g. Dividing the solute mass (5.17 g) by the solution mass (94.91 g) and multiplying by 100 gives the percentage of solute (5.45%).
Of the four concentration units we have looked at, only molarity is a volume based unit. The volume of the solution, in liters, appears in the equation defining the unit (see Equation 2). The other units only have masses or moles in their definitions. Using a substance's molecular weight, you can covert grams to moles and moles to grams, so the mole is also a "mass based" unit. Density is the ratio of mass to volume, that is,
m
d = ----- (Eq.
12)
V
Since mass and volume are fundamentally different physical properties, it is not possible to convert from one to the other unless the density is known. Density is the bridge that allows us to go back and forth between these two physical quantities. To convert from molarity to any of the other units (molality, mole fraction, or mass percent of solute) it will be necessary to know the density of the solution, because the conversion changes a volume based unit to a mass based unit. Likewise, to go from molality, mole fraction, or mass percent of solute to molarity, the density of the solution is needed because the conversion changes a mass based unit to a volume based unit. However, if the conversion does not involve molarity, it is not necessary to know the density of the solution, because the conversion will be entirely concerned with mass based units. Volume never enters the picture.
Concentration unit conversions are somewhat more complicated than the unit conversions you learned about in General Chemistry I. But if you understand the meaning of the concentration units, you should be able to readily do the the conversions after a little exposure to the methods by which these conversions are carried out. Presented below are several worked out examples for you to study.
Example 1: What is the molality of 1.75 M solution of Na2CO3 in water? The density of this solution is 1.112 g/mL.
Since the solution concentration is a ratio (of solute to solvent) it should not depend on how much or how little solution we take. However, depending on the problem being solved, some quantities of solution may be more convenient to work with than others. A strategy that often works in concentration unit conversions is to take an amount of solution that makes the denominator equal to 1 in the definition of the concentration unit that is given. In this problem, we are given the molarity of the solution, so we want to take 1 L of solution. Recall that the equation defining molarity is
# of moles of solute
Molarity =
--------------------
(Eq. 2)
# of liters of solution
Assuming 1 L of solution and substituting the known molarity (1.75 M or 1.75 mol/L), we have
# of moles of solute
1.75 mol/L =
--------------------
(Example 1 Eq. 1)
1 L
Looking at Example 1 Eq. 1, it should be clear that the equation is satisfied only if
# of moles of solute = 1.75 mol (Example 1 Eq. 2)
We now turn to the definition of molality, the unit we are trying to find. Recall that the equation for molality is
# of moles of solute
Molality =
----------------------- (Eq. 3)
# of kg of solvent
We have already determined that our 1 L sample of solution contains 1.75 moles of solute, so we now have
1.75 mol
Molality =
----------------------- (Example 1 Eq.
3)
# of kg of solvent
If we can determine the number of kg of solvent (which is H2O) in this solution, we can calculate the molality by substituting this value into Example 1 Eq. 3 above. To calculate the mass of solvent, we subtract the mass of solute from the mass of solution.
The solute is Na2CO3, and we have 1.75 moles of it. The mass of this solute is
106.0 g
1.75 mol x ------------- = 185.5
g
1 mol
The mass of the solution can be calculated from its density. We have 1 L of solution, or 1000 mL.
1.112 g
1000 mL x ------------- = 1112 g
1 mL
We now know the mass of the solution and the mass of solute (Na2CO3) it contains. The mass of the solvent (H2O) is the difference in these two masses:
mass of H2O = mass of solution - mass of Na2CO3
= 1112 g - 185.5 g = 926.5 g = 0.9265 kg
We can now substitute this mass into Example 1 Eq. 3 to obtain
1.75
mol
Molality = ---------------
= 1.89 m
0.9265 kg
Example 2: What is the molarity of a 2.55 m solution of KI in water? The density of this solution is 1.254 g/mL.
Let us again use the strategy of choosing an amount of solution that makes the denominator equal to 1 in the equation defining the concentration unit that is given. In this case, the molality is given, for which the defining equation is
# of moles of solute
Molality =
----------------------- (Eq. 3)
# of kg of solvent
Therefore, we want to take an amount of solution that will include 1 kg of solvent (which is H2O). Notice that it is not the solution that should have a mass of 1 kg but just the solvent (H2O). The solution will weigh more than 1 kg because of the mass of solute (KI) contained in the solution will add additional mass. Substituting the 1 kg and the known molality (2.55 m or 2.55 mol/kg) into Eq. 3, we have
# of moles of solute
2.55 mol/kg = -----------------------
(Example 2 Eq. 1)
1 kg
Notice that Example 2 Eq. 1 can only be satisfied only if
# of moles of solute = 2.55 mol (Example 2 Eq. 2)
We now turn to the definition of molarity, the unit we are trying to find. Recall that
# of moles of solute
Molarity =
--------------------
(Eq. 2)
# of liters of solution
We already know that our solution contains 1 kg of H2O and 2.55 moles of KI. We can substitute the moles of solute (KI) into Eq. 2 above to obtain
2.55 mol
Molarity =
----------------------
(Example 2 Eq. 3)
# of liters of solution
All that is needed now is to find the number of liters of solution. Once that is known, it can be substituted into Example 2 Eq. 3 to calculate the molarity. To find the volume of the solution, we will make use of the mass and the density. The mass of the solution can be calculated by the mass of solvent (H2O) and solute (KI). We chose to work with a solution contain 1 kg (that is, 1000 g) of solvent (H2O). So if we now calculate the mass of KI in the solution, we can add that to the mass of H2O and get the total mass of the solution. We know our solution contains 2.55 moles of KI, and we can easily convert that into grams:
166.0 g
2.55 mol x ----------- = 423.3
g
1 mol
Therefore,
mass of solution = mass of H2O + mass of KI
= 1000 g + 423.3 g = 1423.3 g
The density of the solution can be used as a conversion factor to go from mass to volume:
1 mL
1423.3 g x -------------- = 1135
mL = 1.135 L
1.254 g
We can now substitute this volume into Example 2 Eq. 3 to obtain
2.55 mol
Molarity =
------------ = 2.25 M
1.135 L
Example 3: What is the mole fraction of KI in a solution that is 0.273 m KI?
As in previous problems, the a good working strategy is to choose an amount of solution that makes the denominator equal to 1 in the equation defining the concentration unit that is given. Here, molality is given, for which the defining equation is
# of moles of solute
Molality =
----------------------- (Eq. 3)
# of kg of solvent
Therefore, we choose an amount of solution that includes 1 kg of solvent (H2O). The molality is already given to be 0.273 mol/kg, so our equation now becomes
# of moles of solute
0.273 mol/kg =
----------------------- (Example
3 Eq. 1)
1 kg
Example 3 Eq. 1 is satisfied only if
# moles of solute = 0.273 mol (Example 3 Eq. 2)
We now turn to the definition of mole fraction, the unit we are trying to calculate. Recognizing that the solvent is H2O and the solute is KI, we can write the equation for the mole fraction of KI as
nKI
XKI = ----------------
(Example 3 Eq. 3)
nKI + nH2O
We already know from Example 3 Eq. 2 that the number of moles of KI is 0.273 mol. All we need now is the number of moles of H2O and we will have everything we need to calculate the mole fraction of KI. We chose an amount of solution that included 1 kg or 1000 g of H2O, and we can easily convert this mass of H2O into moles of H2O.
1 mol
1000 g x ------------
= 55.49 mol
18.02 g
nKI
0.273
mol
0.273 mol
XKI = ---------------
= ----------------------------- =
-------------- = 0.00490
nKI + nH2O
0.273 mol + 55.49 mol 55.763
mol
Note that mole fraction has no units, because the mol units cancel.
Example 4: What is the molality of NaCl in an aqueous solution in which the mole fraction of NaCl is 4.24 x 10-2?
As usual, a good strategy is to base the calculation on an amount of solution that makes the denominator equal to 1 in the equation defining the concentration unit for which the value is given. In this case, the mole fraction is given. Recognizing that the solute is NaCl and the solvent is H2O, we can write the mole fraction for this problem as
nNaCl
XNaCl = -----------------
(Example 4 Eq. 1)
nNaCl + nH2O
Looking at Example 4 Eq. 1, we see that making the denominator equal to 1 requires taking an amount of solution that includes a total of 1 mole of substances, not 1 mole of NaCl or H2O. If the denominator is equal to 1 mol in Example 4 Eq. 1, then the mole fraction of NaCl must be equal to the number of moles of NaCl. We already know that the mole fraction of NaCl is 4.24 x 10-2, so we can write the following:
XNaCl = nNaCl = 4.24 x 10-2 (Example 4 Eq. 2)
Since the NaCl and H2O together account for 1 mol, and the number of moles of NaCl is known, the number of moles of water can be calculated by difference.
number of moles of H2O = 1 mol - number of moles of NaCl
= 1 mol - 4.24 x 10-2 mol
= 0.9576 mol (Example 4 Eq. 3)
We now consider the molality, the unit we are trying to calculate. Recognizing that the solute is NaCl and the solvent is H2O, we can write the molality as
# of moles of NaCl
Molality = ---------------------
(Example 4 Eq.4)
# of kg of H2O
We already know the number of moles of NaCl (which is 4.24 x 10-2) so if we can determine the number of kilograms of H2O, we will have everything we need to calculate the molality of NaCl in the solution. We can calculate the number of kilograms of H2O from the number of moles of H2O.
18.02 g
0.9576 mol x ----------
= 17.26 g = 0.01726 kg
1 mol
Finally, substituting the moles of NaCl and kilograms of H2O into Example 4 Eq. 4 gives the following:
# of moles of solute
4.24 x 10-2 mol
Molality =
----------------------- =
------------------- = 2.46 m
# of kg of solvent
0.01726 kg
In the above answer, the unit m is an abbreviation for mol/kg.
Example 5: What is the molality of a 15.21% C12H22O11 solution?
When a percentage is given, the best strategy is to base the calculation on 100 g of solution. From the definition of percentage (parts per hundred), it is clear that 100.00 g of a 15.21% C12H22O11 solution should contain 15.21 g of C12H22O11. Since the total solution mass is 100.00 g, and 15.21 g of this mass is known to be C12H22O11, the mass of H2O can be calculated by difference.
mass of H2O = mass of solution - mass of C12H22O11
= 100.00 g - 15.21 g
= 84.79 g = 0.08479 kg
The number of moles of C12H22O11 can be calculated from the mass of C12H22O11.
1 mol
15.21 g x ---------
= 0.04443 mol
342.3 g
Now that we have the moles of solute (C12H22O11) and kilograms of solvent (H2O), we can calculate the molality.of C12H22O11 in the solution.
# of moles of C12H22O11
0.04443 mol
Molality =
---------------------------- =
---------------- = 0.5240 m
# of kg of solvent
0.08479 kg
In the above answer, the unit m is an abbreviation for mol/kg.
Example 6: What is the percent by mass of KCl in a 1.53 m KCl solution?
Unless told otherwise, we assume the solvent is H2O. Since molality is given, we want to base the calculation on an amount of solution that includes 1 kg (that is, 1000 g) of H2O (solvent). The molality of KCl in this solution can be written as follows:
# of moles of KCl
# of moles of KCl
Molality =
----------------------- =
---------------------- (Example
6 Eq. 1)
# of kg of H2O
1 kg
Since the denominator is 1 in Equation 6 Eq. 1, the number of moles of KCl must be numerically equal to the molality, which is given to be 1.53 m.
The mass of 1.53 moles of KCl is calculated as follows:
74.55 g
1.53 mol x -----------
= 114.1 g
1 mol
We now know the mass of KCl (which is 114.1 g) and the mass of H2O (which is 1000 g), so we can calculate what percent of the the solution's mass is due to KCl.
mass of solution = mass of H2O + mass of KCl
= 1000 g + 114.1 g
= 1114.1 g
mass of solute
114.1 g
Mass% solute = 100% x
------------------- = 100%
x ----------- = 10.2%
mass of solution
1114.1 g
Example 7: What is the mole fraction of NaI in a solution that is 17.85% NaI by mass?
Since a percentage is given, a good approach is to base the calculation on 100 g of solution. From the definition of percentage (parts per hundred), we know that a 100.00 g sample of a 17.85% NaI solution will contain 17.85 g of NaI. Since the chemical identity of the solvent is not specifically stated, it is assumed to be H2O. Since the solution has a mass of 100.00 g and we know it contains 17.85 g of NaI, we can calculate the mass of H2O by difference.
mass of H2O = mass of solution - mass of NaI
= 100.00 g - 17.85 g
= 82.15 g
We now have the mass of both the H2O and the NaI. We need the number of moles of each in order to calculate the mole fraction of NaI. We can easily convert from grams to moles.
1 mol
82.15 g x ----------
= 4.559
mol (for H2O)
18.02 g
1 mol
17.85 g x ----------
= 0.1191 mol
(for NaI)
149.9 g
Now the mole fraction of NaI can be calculated.
nNaI
0.1191
mol
0.1191 mol
XNaI =
------------------ =
--------------------------- =
-------------- = 0.02546
nNaI + nH2O
0.1191 mol + 4.559
mol 4.6781
mol
Example 8: What is the percent by mass of HCl in a solution in which the mole fraction of HCl is 1.48 x 10-2?
Since the chemical identity of the solvent is not given, we assume it is H2O. The equation for the mole fraction of HCl in this solution is
nHCl
XHCl =
---------------------- (Example 8 Eq.
1)
nHCl + nH2O
As usual, it is convenient to work with an amount of solution that makes the denominator equal to 1 in the equation defining the concentration unit for which the value is given. In this problem, the mole fraction is given, so we want the denominator to be 1 mol in Example 8 Eq. 1 above. That is, the total number of moles of HCl and H2O together will be 1 mol. If that's the case, then the mole fraction of HCl must be numerically equal to the number of moles of HCl. Therefore, there are 1.48 x 10-2 moles of HCl in the solution. Since the total number of moles is 1 mol, and the number of moles of HCl is known, the number of moles of H2O can be found by difference.
nH2O = ntotal - nHCl
= 1 mol - 1.48 x 10-2 mol
= 0.9852 mol (Example 8 Eq. 2)
We want to calculate the percent by mass of HCl in the solution. This is given by
mass of HCl
Mass% HCl = 100% x
-------------------
(Example 8 Eq. 3)
mass of
solution
We know the moles of HCl (1.48 x 10-2) and the moles of H2O (0.9852) and these can be converted to grams for use in Example 8 Eq. 2.
36.46 g
1.48 x 10-2 mol x --------------
= 0.5396 g (for HCl)
1 mol
18.016 g
0.9852 mol x ----------- =
17.749 g (for H2O)
1 mol
mass of solution = mass of HCl
+ mass of H2O
(Example 8 Eq. 4)
= 0.5396 g
+ 17.749 g
= 18.2886 g
Now, substituting the appropriate masses from Example 8 Eq. 4 into Example 8 Eq. 3, we have
0.5396 g
Mass% HCl = 100% x
------------- = 2.95%
18.2886
g
Example 9: What is the molarity of NaCl in a solution that is 5.02% NaCl by mass? The density of this solution is 1.028 g/mL.
Since the mass percentage of NaCl is given, let's assume we have 100.00 g of solution. In this amount of solution, we will have 5.02 g of NaCl, because the percentage is the number of "parts" (in this case grams) of solute in 100 "parts" (again, grams) of solution.
We are looking for the molarity of NaCl in this solution. The equation for molarity is
# of moles of solute
Molarity =
----------------------
(Eq. 2)
# of liters of solution
We need the number of moles of NaCl and the number of liters of solution to calculate the molarity in Eq. 2 above. We can convert the 5.02 g of NaCl to moles of NaCl, and use the density of the solution (1.028 g/mL) to calculate the volume of the solution.
1 mol
5.02 g x ---------- = 0.08590
mol
58.44 g
1 mL
100 g x --------- = 97.276
mL = 0.097276 L
1.028 g
0.08590 mol
Molarity =
-------------- = 0.883
mol/L = 0.883 M
0.097276 L
Example 10: What is the percent by mass of CaCl2 in a 2.78 M CaCl2 solution? The density of this solution is 1.165 g/mL.
The molarity of the solution is given, so let's start with the definition for molarity:
# of moles of solute
Molarity =
----------------------
(Eq. 2)
# of liters of solution
We already know that the molarity is 2.78 mol/L. If we assume a solution volume of 1 L, then we can write the following equation:
# of moles of CaCl2
2.78 mol/L =
------------------------- (Example 10 Eq. 1)
1 L
Example 10 Eq. 1 is satisfied only if
# of moles of CaCl2 = 2.78 mol (Example 10 Eq. 2)
To calculate the mass percent of solute (which is CaCl2), we need to use the following equation:
mass of solute
Mass% solute = 100% x
-------------------
(Eq. 9)
mass of solution
We need to convert the 2.78 mol of CaCl2 to grams of CaCl2 and use the density of the solution to calculate its mass.
110.98 g
2.78 mol x ----------- = 308.52
g (mass of solute)
1 mol
We have 1 L of solution, which is the same thing as 1000 mL.
1.165 g
1000 mL x ------------ =
1165 g (mass of solution)
1 mL
308.52
g
Mass% solute = 100% x
------------ = 26.5%
1165 g
Example 11: What is the mole fraction of HCl in a 3.48 M HCl solution? The density of the solution is 1.058 g/mL.
The molarity is given. Molarity is defined by the following equation:
# of moles of solute
Molarity =
--------------------
(Eq. 2)
# of liters of solution
If we assume 1 L of solution, then we can write the following equation:
# moles of HCl
3.48 mol/L =
------------------- (Example 11
Eq. 1)
1 L
Example 11 Eq. 1 is satisfied only if
# moles of HCl = 3.48 mol (Example 11 Eq. 2)
Now consider the equation for mole fraction:
nsolute
Xsolute =
---------------------- (Eq. 5)
nsolute + nsolvent
Here, HCl is the solute and H2O is the solvent, so we have
nHCl
XHCl =
---------------------- (Example 11 Eq.
3)
nHCl + nH2O
We already know there are 3.48 moles of HCl, but we don't know the number of moles of H2O. However, we know we have 1 L of solution, and we know the density of the solution. From this information, we can calculate the mass of the solution, and by subtracting the mass of HCl (which we can calculate from the number of moles of HCl) we can find the mass of the H2O. Then we can convert the mass of H2O to moles of H2O.
1.058 g
1000 mL x ----------- = 1058
g (mass of
solution)
1 mL
36.46 g
3.48 mol x ------------ = 126.88g
(mass of HCl)
1 mol
Mass of H2O = mass of solution - mass of HCl (Example 11 Eq. 4)
= 1058 g - 126.88 g = 931.12 g
1 mol
931.12 g x ----------
= 51.683 mol
18.016 g
Now we know the moles of both HCl (3.48 mol) and H2O (51.683 mol) and these values can be substituted into Example 11 Eq. 3.
3.48
mol
3.48 mol
XHCl =
------------------------ =
-------------- =
0.0631 or 6.31 x 10-2
3.48
mol + 51.683 mol
55.163 mol
Example 12: What is the molarity of a NaCl solution in which the mole fraction of NaCl is 9.11 x 10-3? The density of the solution is 1.016 g/mL.
The equation for mole fraction is
nsolute
Xsolute =
---------------------- (Eq. 5)
nsolute + nsolvent
In this problem, the solute is NaCl and the solvent is H2O. With this in mind, we can write
nNaCl
XNaCl =
---------------------- (Example 12 Eq.
1)
nNaCl + nH2O
As we have seen, a strategy that frequently works is to assume an amount of solution that makes the denominator equal to 1 in the definition for the concentration unit that is given. So in this problem, we assume a total amount of solution of 1 mole. That's not 1 mole of NaCl or 1 mole of H2O but 1 mole total. That is,
nNaCl + nH2O = 1 mol (Example 12 Eq. 2)
Substituting Example 12 Eq. 2 into Example 12 Eq. 1, we get
nNaCl
XNaCl =
--------
(Example 12 Eq. 3)
1
mol
Notice that Example 12 Eq. 3 is only satisfied if the number of moles of NaCl is numerically equal to the mole fraction of NaCl. The mole fraction and number of moles can not truly be equal, because mole fraction is dimensionless and number of moles has a unit, but the numerical values are the same. Therefore
nNaCl = 9.11 x 10-3 mol (Example 12 Eq. 4)
Since the total number of moles is 1 mol, and the number of moles of NaCl is now known, the number of moles of H2O can be found by difference:
nH2O = ntotal - nNaCl (Example 12 Eq. 5)
= 1 mol - 9.11 x 10-3 mol = 0.99089 mol
The masses of NaCl and H2O in the solution are as follows:
58.44 g
9.11 x 10-3 mol x ---------
= 0.5324
g
(mass of NaCl)
1 mol
18.016 g
0.99089 mol x ---------- = 17.852
g
(mass of H2O)
1 mol
The solution mass is the sum of these two masses:
Mass of solution = mass of NaCl + mass of H2O (Example 12 Eq. 6)
= 0.5324 g + 17.852 g = 18.3844 g (mass of solution)
Now that the mass of solution is known, we can use the density to calculate its volume:
1 mL
18.3844 g x --------- =
18.095 mL = 0.018095 L
1.016 g
The equation for molarity is
# of moles of solute
Molarity =
--------------------
(Eq. 2)
# of liters of solution
In this problem, we have 9.11 x 10-3 moles of NaCl (solute) and 0.018095 L of solution.
9.11 x 10-3 mol
Molarity = -----------------
= 0.503 mol/L
0.018095 L
This page was last modified Monday July 18, 2005.