In chemistry, as in many branches of science, we shall have occasion to deal with both qualitative and quantitative descriptions of the world around us. A statement such as "it's cold in this room" is an example of a qualitative statement. A qualitative attribute is one which expresses some characteristic without placing it on any scale of measure. The above statement about the room tells us it is cold rather than hot, but does not tell us how cold it is.
Suppose, however, that I tell you "it is 18 oC in this room". I have now placed the degree of "coldness" (or "hotness") on a numerical scale. Those who are not even in the room can get an idea what the room environment is like if they are familiar with the Celcius temperature scale. Furthermore, the numerical scale allows one to make comparisons. A room where the temperature is 28 oC will likely be felt as warmer than one at 18 oC, even if differences in humidity are factored in.
My statement of the temperature in the room is a quantitative statement. A quantitative attribute is one which expresses the degree or magnitude of some characteristic by assigning it a value on some comparative scale of measure. Although both qualitative and quantitative properties will be important to us in chemistry, we will find that we deal with the quantitative features of chemistry more often than the qualitative ones.
Dimensionless and Dimensional Quantities
In the previous section, we saw that our observations could be divided into those that were qualitative in nature, and those that were quantitative in nature. Further, we saw that we would deal more often with observations of a quantitative nature.
Focusing our attention on quantitative properties, we find that we can again subdivide them -- we can specify a quantitative parameter as being either dimensionless or dimensional.
Dimensionless quantities are pure numbers such as 3, 5.87, and 3/4 ("three fourths"). Dimensional quantities are those that carry units, such as 11.5 m, 5 hours, and 1.50 g. The units are a part of the quantity and it is incorrect to report a dimensional quantity without its associated units. For example, suppose I told you I had a roll of copper wire and you asked me how long it was. If I merely told you "22" you would still not know the length of the wire. Do I mean 22 inches? feet ? meters? . . . and so on. As this example makes clear, I must specify both a number and a unit or I have not told you anything.
The term dimension refers -- in a generic way -- to the attribute one is physically measuring. The dimension of length, for example, is very different from the dimension of temperature. Once we settle on a particular dimension we want to measure, there is a choice of several units we might use to express the magnitude of that dimension. Thus, if measuring length, we might use inches, feet, centimeters, or meters. If measuring temperature, we could use Fahrenheit, Celcisus, or Kelvin. The variety of units available means it will sometimes be necessary to convert from one unit to another.
The dimensions mentioned in the pervious paragraph -- length and temperature -- are elementary dimensions in the sense that they can not be broken down into simpler dimensions. Other dimensions -- lets call them compound dimensions -- can be built using these elementary dimensions.
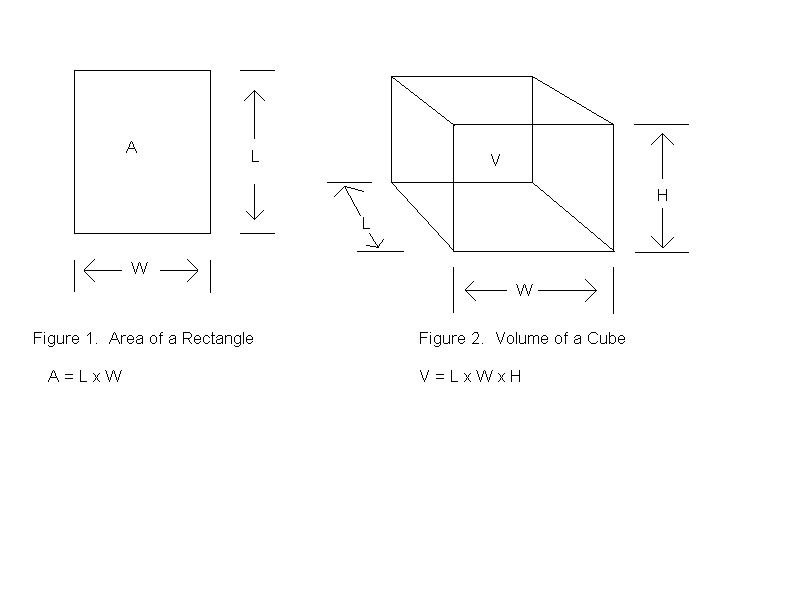
For example, the dimension of speed is a compound dimension, being made up of the length and time dimensions. Mathematically, speed has dimensions of length / time. In the United States, we use the mile as the unit of length and the hour as the unit of time when measuring the speed of our cars. In most other countries we would measure the speed in units of kilometers / hour. Thus, we have a choice of units to use for measuring compound dimensions, just as we do for measuring elementary dimensions. Other compound dimensions that will be important to us are area, which has dimensions of length2, and volume, which has dimensions of length3. The origin of these dimensions can be explained by considering two simple geometric figures -- the rectangle and the cube. The area of a rectangle is calculated by multiplying its length by its width. Since both of these have dimensions of length, we end up multiplying length by itself, which gives length2 (see Figure 1). Similarly, we calculate the volume of a cube by multiplying it length, width, and height. Since all of these have dimensions of length, we end up multiplying length x length x length, which gives length3 (see Figure 2).

Why not just adopt one unit for each dimension we want to measure, so unit conversions would not be necessary? Well, suppose we adopt the inch as the unit we will use to express all lengths. Can you quickly get a perception of how far I live from Palo Alto if I tell you the distance is about 1,267,000 inches? If, rather than using inches, I tell you I live 20 miles from Palo Alto, you immediately get a good idea of the distance. On the other hand, the mile would not be a convenient unit of length to use when measuring the width of your window for a new set of curtains. When making measurements, it is desirable to use a unit that has a size that is comparable to the quantity being measured. But there may be more than one unit that is a "good" size to use, meaning different people may be using different units, and a conversion of units may then be necessary in order for two people to more effectively communicate.
While scientists don't always use the same units (for the reasons given in the preceding paragraph) they have tried to standardize measurements as much as possible by adopting the metric system internationally for all scientific work. The metric system consists of a set of "original" units (or unprefexed units) for each physical dimension, and a set of prefixes that can make the original unit larger or smaller as needed. See Table 1.3 on page 27 in your Kotz 6th Edition textbook for a list of metric prefixes and their meanings. Carefully read Section 1.6, "Units of Measurement on pages 25-32..
What I have called the "original" unit in these notes is often called the base unit in textbooks. When discussing the metric system for the first time, most textbooks use the term "base unit" to mean an unprefixed unit. However, this can cause confusion when we discuss SI units.
The SI system is essentially, an attempt to have just one unit for each possible measurement. There are times when using SI can be convenient, but as discussed two paragraphs earlier, being forced to use a particular set of units for ALL measurements can be rather awkward. The SI system is a subset of the metric system. In the SI system, lengths are always measured in meters, masses in kilograms and times in seconds. Note that in the SI system, the "base" unit of mass is the kilogram -- a unit which already has a prefix. This is why I avoided the use of the term "base unit" in the previous paragraph.
Compound units in the SI are made up of SI base units. Speed in the SI system is measured in meters per second (m/s), area in square meters (m2), volume in cubic meters (m3), and density in kilograms per cubic meter (kg/m3). Many of these units are of an awkward size for conventional laboratory use. For example, a cubic meter is the volume inside a box that is one meter long, one meter wide, and one meter high. (1m x 1m x 1m = 1m3). This is much too large to be convenient for reporting volumes of chemicals used in routine laboratory work. Our unprefixed volume unit for common laboratory work is the liter (L). This is still too large to be convenient in most situations, so we usually use the milliliter (mL). Almost all laboratory glassware is calibrated in mL.
All volume units can ultimately be traced back to a volume unit that has the word "cubic" in its name. We don't hear anything cubic in the word "liter", but a liter is the same volume as a cubic decimeter, that is, 1 L = 1 dm3. Other equivalencies you may sometimes find useful are 1 mL = 1 cm3, 1 m3 = 1000 L, and 1 gal = 231 in3.
Knowing how to get from volume units without the word cubic in their name to those that have the word cubic is important when you are calculating the volume of something using a formula that will only let you obtain an answer in some kind of cubic units. For example, the volume of a sphere is given by the equation V = (4/3) (Pi) r3, where Pi = 3.14159265358979 . . . (non-repeating, non-terminating decimal). The (4/3) and the Pi are dimensionless, and r has dimensions of length. The r gets cubed, so V will have dimensions of length3, which are the dimensions of volume. Lets suppose you wanted to use this formula to calculate the volume of a sphere in liters. Since a liter is equal to a cubic decimeter, you should measure the radius (r) of the sphere in decimeters. That way, when the decimeters get cubed, you will have cubic decimeters, which is the same thing as liters. One the other hand, if you wanted the volume of the sphere in milliliters, you should measure the radius of the sphere in centimeters, because then the volume you calculate will be in cubic centimeters, which is the same thing as milliliters.
With all that as background, its time to actually start doing some unit conversions. Lets start with a simple one. Convert 15 feet to yards. Prior to your exposure to units in this course, many of you may have used a numbers only approach:
15 / 3 = 5
But what if you incorrectly multiplied the two numbers rather than dividing them, that is,
15 x 3 = 45
If you don't think carefully about what you're doing, you might not catch the error. After all, 45 looks like just as good a number as 5. Neither is unusually large or unusually small. As we will see, carrying the units through the calculations will make errors much more obvious, so we can catch them and correct them.
In order to carry out a unit conversion, we take the quantity we start with and multiply it by one or more conversion factors to obtain the quantity we want. We construct our conversion factors from the mathematical relationships between the units involved. In the present example, we know that
1 yd = 3 ft
Mathematically, we can perform any legal operation on an equation as long as the operation is performed on both sides. Suppose we take the equation above and divide both sides by 3 ft.
1 yd = 3 ft
3 ft 3 ft
The quantity on the right hand side is equal to 1, because we have the same thing in both the numerator and denominator. Perhaps having units in the equation is a new feature to you, but after you get used to it, you should find it is second nature to you. You already know this works with pure numbers. For example
2 = 1 3
= 1 4
= 1 and so on.
2
3
4
Extending this principle to quantities with units, we have
1 yd = 1
3 ft
When we work with units in our problems, the units multiply and divide just like ordinary numbers. This includes cancellations. You may have cancelled ordinary numbers when multiplying fractions. For example consider the following fraction multiplication problem:
3 x 2
= 6
4
3 12
Some math teachers will take points off your paper if you don't reduce the answer to 1/2. You can get the reduced fraction as your original answer if you will do some cancellation of numbers. Since 3 appears as both a numerator (in 3/4) and a denominator (in 2/3), the 3 can be cancelled. If we rewrite the 4 (in 3/4) as 2 . 2 we then have a 2 in the denominator that we can cancel with the 2 in the numerator (of 2/3).
3
x 2 =
1
2 . 2
3 2
Both numbers cancelled out on top, but we can imagine one of the numbers being multiplied by 1 (you can always multiply something by one without changing it) which explains the 1 in the numerator of our answer. In the denominator, we cancelled the 3 and one of the two 2's, leaving one that is still there. This explains the 2 in the denominator of our answer. To extend these principles to our work in chemistry, all you have to remember is that units multiply, divide, and cancel just like numbers.
The conversion of 15 feet to yards looks like this:
15 ft x 1 yd
= 5 yd
3 ft
Because units behave just like numbers in calculations, we can cancel them out, just as we did in the previous problem involving only numbers. We have the unit ft in both the numerator and the denominator so it can be cancelled out. We can make it clear that the 15 ft is a numerator quantity by putting it over 1:
15 ft x 1
yd = 5 yd
1
3 ft
When we do unit conversions such as that above, we don't change the starting quantity -- at least, not in a mathematical sense. Certainly, it looks different; 5 yd does not have the same appearance as 15 ft. But since conversions factors are equal to 1, there is no way that multiplying something by a conversion factor can change its mathematical value, even though the answer looks different than what we started with. The conversion factor only makes what I will call a "cosmetic" change -- the new quantity looks different from the original but is mathematically equal to it.
Notice that the question of whether to multiply the 15 by 3 or divide it by 3 does not arise, as it did when only numbers were used in the calculation. The conversion factor has to be arranged a certain way to make the units cancel properly, and the placement of the units shows us where to put the numbers. Everything just falls into place.
But suppose you did make a mistake. You will get an answer with units that make no sense. This is an immediate tip-off that something is wrong. For example, if you wrote the conversion factor upside down, you would get:
15 ft x 3 ft
= 45 ft2
1 yd
yd
We get units of "square feet per yard", which makes no sense.
By the way, the factor 3 ft
is a valid conversion factor, that is, it is equal to 1. It's just
that it's not suited to this particular
1 yd
problem. If you wanted to convert yards to feet, it would be the one to use. Thus, once you have identified one conversion factor, you have really found two conversion factors, because you can always take the one you found and turn it upside down to get another factor. So
1 yd = 1
and 3 ft
= 1
3 ft
1 yd
The unit conversion we just finished was accomplished in a single step -- that is, we only had to use a single conversion factor. There are times, however, when it is more convenient to do the conversion in more than one step, because we can not readily identify the numbers that go in the conversion factor.
Let's say you want to convert 2.85 decimeters to inches (shorthand notation: dm -----> in). Try writing out the conversion, building the conversion factor units first.
2.85 dm x
in =
dm
In the above set-up, the units have been filled in and space has been left for the numbers. It is clear that the units are placed correctly, because only this placement will cause dm to cancel and leave in as the units of the answer. But what numbers belong in the conversion factor? Unless we have this information, the factor is useless. Let's suppose we do not have available to us, the relationship between these units. We will proceed as follows:
From the definition of the prefix deci-, we know that
1 dm = 1 x 10-1 m
and from this, we can get two conversion factors:
1 dm
= 1
and 1 x 10-1
m
= 1
(will need only one of these)
1 x 10-1 m
1 dm
From the definition of the prefix centi, we know that
1 cm = 1 x 10-2 m
and from this we can get two conversion factors:
1 cm
= 1
and 1 x 10-2
m
= 1
(will need only one of these)
1 x 10-2 m
1 cm
The relationship between inches and centimeters is usually reported in English / metric conversion tables:
1 in = 2.54 cm
and from this we can get two conversion factors:
1 in
= 1
and 2.54 cm
= 1
(will need only one of these)
2.54 cm
1 in
With this information, we can devise the following 3-step path to go from decimeters to inches:
dm -----> m -----> cm -----> in
We can use the above "roadmap" to help us write the conversion factors. The process is so definite that we will not even have to look back at the possible conversion factors for the relationships that were given. Everything will just fall into place. Each arrow will be replaced with a conversion factor. Whatever unit appears at the tail of the arrow will be in the denominator of the corresponding conversion factor, and whatever unit appears at the head of the arrow will be in the numerator of the corresponding conversion factor. If properly constructed, each conversion factor will have a denominator with units that cancel those of the previous numerator. At this point we can write
2.85 dm x
m x
cm x
in =
dm
m
cm
In this set up, I have followed the instructions in the above paragraph to write the units in the correct places. All that is left now is to fill in the numbers. The relationships are
1 dm = 1 x 10-1 m
1 cm = 1 x 10-2 m
1 in = 2.54 cm
We can copy the numbers that appear in front of the units in these equations to be in front of the same units in the conversion factors. This gives
2.85 dm x 1 x 10-1
m
x
1 cm x
1 in =
11.2 in
1 dm
1 x 10-2 m
2.54 cm
Notice that we have used one conversion factor from each of the 3 pairs we identified earlier.
A pattern worth noting here is that if a conversion factor has the same fundamental unit in both the numerator and the denominator, with the only difference being that in one case the unit is unprefixed, and in the other case, it has a prefix, we can always put a 1 in front of the unit that has a prefix and put the meaning of that prefix in front of the unit that does not have a prefix.
In the calculation above, you see in the first conversion factor that dm has a 1 in front of it while the meaning of deci, 1 x 10-1 is placed in front of m. Likewise, in the second conversion factor, cm has a 1 front of it and the meaning of centi, 1 x 10-2 is in front of m. The third conversion factor sometimes causes confusion. The unit cm has a prefix -- centi-. Why did we not put a 1 in front of it? We have to recall that this pattern exists only if the same fundamental unit is in both the numerator and the denominator. The only difference can be a prefix or the lack of one. In the third conversion factor, the units are inches and centimeters. These are fundamentally different units, because you can not change one into the other just by adding or removing a prefix. In cases like this, you have to look at the relationship between the units, rather than attempting to blindly follow some pattern.
One problem that students have in working out the above calculation is that many don't know how to properly enter numbers in scientific notation in their calculator. You should not explicitly multiply by the 10 shown in such numbers. Rather, a key on your calculator usually labeled either EE or EXP should be used. This is discussed on page 37 of your Kotz book in the box at the top of page 37 ("Problem-Solving Tip 1.2").
A number in scientific notation has two parts: the first part, called the mantissa, is the number that comes before the x 10, and the second part, called the exponent, is the power to which the 10 is raised.
For example, the scientific notation number 7.52 x 10-5 has a mantissa of 7.52 and an exponent of -5. It is entered in a scientific calculator as 7.52 EE -5. If this number was displayed as an answer by a calculator or computer, it might appear as 7.52E-5. (see the text near the bottom of page 37.) It is important for you to understnad this notation, since you will need to work with such numbers when doing online homework, and when using your scientific calculator.
If you have a scientific notation number that seems to have no mantissa -- only an exponent -- the mantissa is equal to 1. For example 104 is the same thing as 1 x 104. It is important to keep this in mind because your calculator will always "want" you to enter both the mantissa and the exponent.
Another error students sometimes make in working out a string of conversion factors such as that above is separating entries with the multiplication key when the division key should be used. For our conversion of dm to in, the following are correct calculations:
2.85 x 1 x 10-1 / 1 x 10-2 / 2.54 = 11.2
2.85 x 1 x 10-1 / ( 1 x 10-2 x 2.54 ) = 11.2
But the following is INCORRECT:
2.85 x 1 x 10-1 / 1 x 10-2 x 2.54 = 72.4
You may want to convince yourself of this by using numbers that are more common. Try the following. It should be clear that
4 x 3
= 12 =
2
3
2
6
How could you enter these numbers into a calculator and get 2 as the answer?
4 x 3 / 3 / 2 = 2
and
4 x 3 / ( 3 x 2 ) = 2
but
4 x 3 / 3 x 2 = 8 <-----WRONG ANSWER!
So, when working out conversion factors, first enter all numbers in the numerator, separating them with the multiplication key, press the division key after you have entered the last number in the numerator, then enter all the numbers in the denominator, separating them with the division key. If you want to separate the denominator numbers with the multiplication key, you must enclose them in parentheses, as the above examples show.
One final thing I would like to address in these notes is conversions involving squared or cubic units. Sometimes students overlook the fact that if the units are squared or cubed, rather than linear, the relationship between the units is also squared or cubed. We know that there are 3 feet in a yard, and students sometimes make the mistake of assuming that there must likewise be 3 square feet in a square yard. This is not the case. There are actually 9 square feet in a square yard. We can show this in three ways. Perhaps the most direct way is to start with the relationship between the linear units:
1 yd = 3 ft
Then, realizing we can perform any valid mathematical operation on an equation if we perform it on both sides, we square both sides of the equation to get
1 yd2 = 9 ft2
Another way to see this equivalence is to measure the sides of a square yard in both yard and feet units and calculate the area in each case. A square that is one yard long on all sides is by definition, a square yard. Measuring this same square in feet shows that the area is also 9 square feet (See Figure 3).
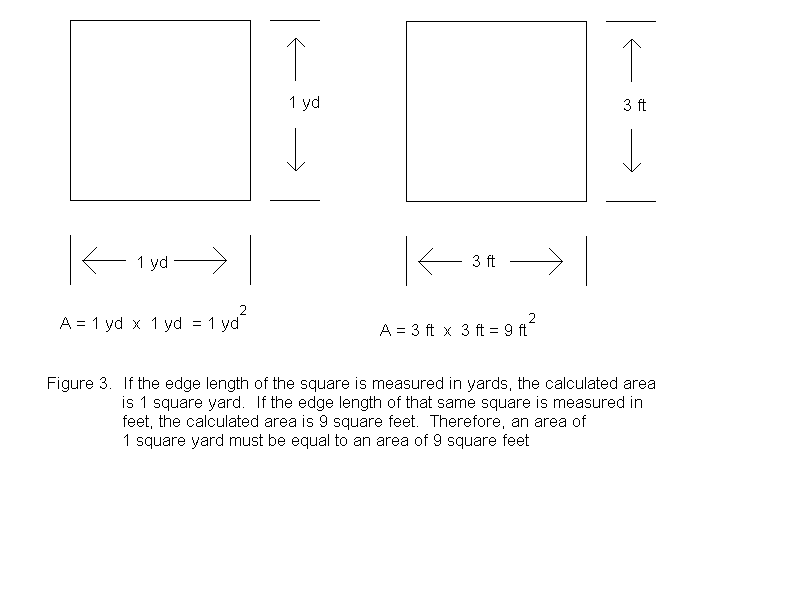
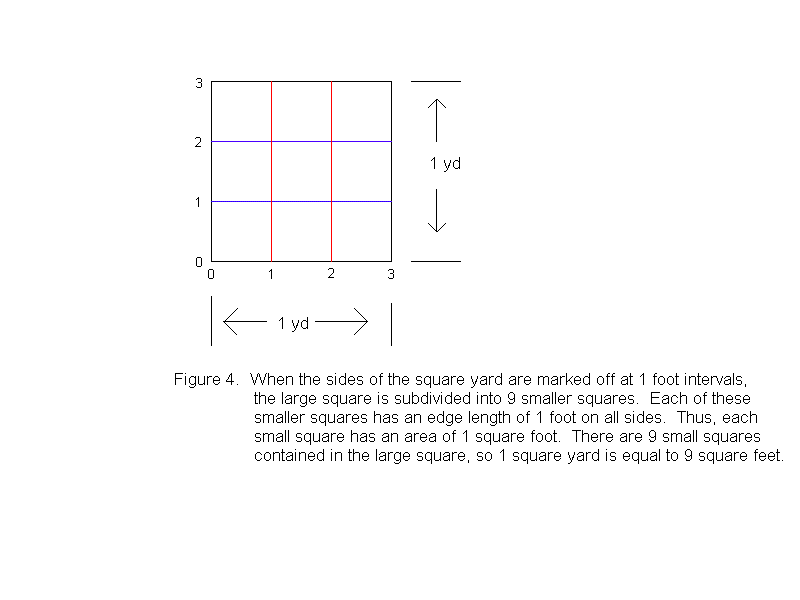
Yet another way to see that one square yard is 9 square feet is to
mark off the sides of the square yard at one foot intervals. This
divides the square yard (large square) into 9 smaller squares that each
have an area of 1 square foot (See Figure 4).
Now let's do a unit conversion problem involving square units: Convert an area of 432 square inches into square feet. We proceed by first constructing the necessary relationship between the squared units. We can obtain this from the linear relationship. We know that
1 ft = 12 in
We square both sides of this equation to get
1 ft2 = 144 in2
from which we can obtain the conversion factors
1 ft2
= 1
and 144 in2
= 1
(only one of which will be used)
144 in2
1 ft2
Since we want to convert in2 to ft2, we need to have in2 in the denominator for proper cancellation of units. The calculation therefore looks like this:
432 in2 x
1
ft2
= 3 ft2
144 in2
Page Updated Tuesday August 29, 2006/