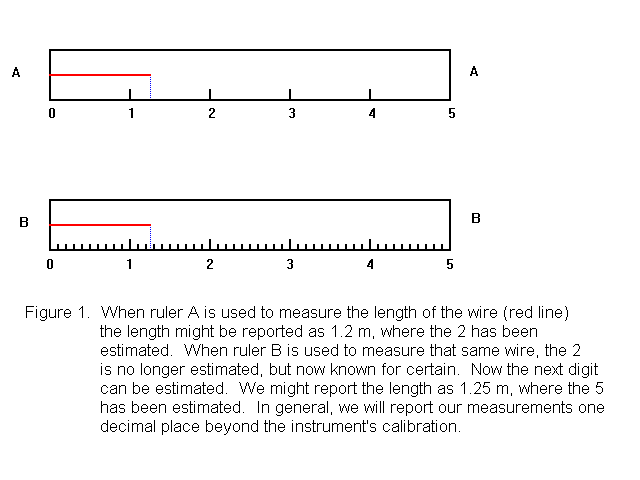
The value of a numerical quantity is obvious from looking at it, but how do we know the uncertainty? If I report the length of a wire as 1.2 m, I am saying that the length of the wire appears to be "about 1.2 m". I can not say the length of the wire is exactly 1.2 m, because it is not possible to make measurements with complete certainty. Measurements are normally reported in such a way that the uncertainty lies in the last (right-most) digit that is reported. Typically, we assume the uncertainty in that last digit is plus or minus one unit.
Applying this to our example above, we assume the true value of the length is somewhere between 1.1 m and 1.3 m, with 1.2 m being our best estimate. We can consider each digit in a reported measurement to be either a centain digit or an uncertain (sometimes called doubtful) digit. In the value 1.2 m, the 1 is a certain digit. We are completely sure the digit immediately before the decimal point is a 1. The 2 is an uncertain digit, however. We say it has been estimated. This is illustrated in Figure 1, when the wire (shown as a red line) is measured with ruler A. The significant figures in a measured quantity include all the digits that we know for sure, plus one that is uncertain (estimated). (An exception is zeros at the beginning of a number. These are known for sure, but are not significant) To report a measured number to the correct number of significant figures, you should include one uncertain digit -- but only one -- in your number. We say the number 1.2 m has two significant figures.

Notice that the device used to make a measurement determines how precisely we can make our measurements. Ruler A is marked off in increments of 1 m, and this makes it possible for us to measure lengths to the nearest 0.1 m, because we can estimate between calibration marks. Ruler B, however, is marked off in increments of 0.1 m, and this makes it possible for us to measure lengths to the nearest 0.01 m, again, because we can estimate between calibration marks. With ruler B, we can report a length such as 1.25 m, where the 1 and the 2 are certain digits and the 5 is uncertain. We say the number 1.25 m has three significant figures.
Suppose when using Ruler B to measure a wire, the wire seems to end right at the 1.2 calibration mark, rather than ending somewhere between the marks. Then is it ok to report the value as 1.2 m? No! Because this would imply that the uncertainty was about plus or minus 0.1 m. That is, that the actual value could be anywhere in the range 1.1 m to 1.3 m. But in fact, this ruler lets us estimate to plus or minus 0.01 m. So if the wire appears to end at the 1.2 mark, we report the length as 1.20 m. Expressed this way, the number tells is that the actual length is expected to be somewhere in the range 1.19 m - 1.21 m, and 1.20 m is our best estimate (See Figure 2).

When you have the measuring device available to you -- as we do in these notes -- you can determine how many significant figures your measurements will have by looking at the device. Many times, however, we have to rely on measurements reported by others, and we don't have access to their measuring device. Assuming the person who made the measurement reported it correctly, there are a few simple rules we can use to determine how many significant figures are in a measurement. Remember, these rules are for direct measurements ONLY. There will be other rules for calculation results, or for things that are counted or defined, rather than measured.
Rules for Directly Measured Data:
Now for some examples:
1.2 m has 2 significant figures; 1.25 m has 3 significant figures (rule 1).
0.0027 g has 2 significant figures (rules 1 and 2).
6.000 m has 4 significant figures (rules 1 and 3)
10.002 g has 5 significant figures (rules 1, 3, and 4)
0.0050 g has 2 significant figures (rules 1, 2, and 3)
50.0500 g has 6 significant figures (rules 1, 3, and 4)
500 m has an indeterminate number of significant figures (rule 5)
Regarding the last examle, we can be sure it has at least one significant figure, because the 5 has to be significant (by rule 1). But we can't tell about the two zeros (rule 5). It might be that the number is very poorly known -- that the true value lies somewhere between 400 m and 600 m, with 500 m as the best estimate. In other words, only known to the nearest hundred. In this case, only the 5 is a significant figure and we say the number has one significant figure. Or, perhaps the first zero is significant but not the second. In other words, the number is known to the nearest ten. The actual value is somewhere between 490 and 510, with 500 being our best estmate. In this case we say the number has 2 significant figures. Finally, the last possibility is that both zeros are significant. In this case, the number is known to the nearest unit, that is, somewhere between 499 and 501, with 500 being our best estimate. Here, we say the number has 3 significant figures. The only possibilities are 1, 2, or 3 significant figures. There is no way it could have 4 significant figures, since nothing is reported beyond the decimal point -- which is assumed to be at the right end of the number, since no decimal point is shown.
When digits are not significant, we try to avoid writing them. With zeros, however, we are sometimes forced to write them even when they are not significant. If the number 500 has only one significant figure and I don't write the zeros, it will look like 5 m instead of 500 m. But there is a BIG difference between 5 m and 500 m! If the zeros are not significant, we say they are written to "locate the position of the decimal point". Another way to say this is that they are written to indicate the size of the number. Since the zeros would have to be written whether or not they are significant -- just to make the number the right size -- we can't tell just by looking whether or not they are significant. A quick way to indicate that a number ending in zeros is known to the nearest unit -- that is, that all the zeros are significant -- is to explicitly show the decimal point. Thus 500. m has 3 significant figures but 500 m (no decimal point shown) has an indeterminate number of significant fiugres (either 1, 2, or 3).
Applying the rule that we avoid writing digits that are not significant whenever possible, you can understand why zeros that appear after a decimal point are significant (unless they qualify as being at the beginning of a number). Zeros to the right of a decimal point do not change the size of a number, only the precision with which it is known. For example, 5 m, 5.0 m, and 5.00 m all represent the same nominal length. But 5 m is "five meters give or take about a meter", 5.0 m is "five meters give or take about a tenth of a meter" and 5.00 m is "five meters give or take about a hundredth of a meter". Unlike the writing of the number 500 m, where the zeros had to be there to indicate the size of the number, in the case of five meters, we would not write them unless they really were significnat, because leaving them off does not change the size of the number. Therefore, if a measured length is reported as 5.00 m, you know both zeros are significant and the number has 3 significant figures. The actual value is believed to be somewhere in the range 4.99 m and 5.01 m.
A student in one of my classes asked an excellent question: why are the leading zeros in a number not significant? After all, 0.5 g is known to plus or minus 0.1 g, and 0.0005 g is known to plus or minus 0.0001 g. Doesn't that mean the second number (0.0005 g) is known more precisely than the first (0.5 g)? At first glance, it sure would seem to be the case, but we can show that both numbers actually have the same precision.
Consider the relative error in these numbers. If we assume the quantity 0.5 g can vary by up to 0.1 g above or below its nominal value, then the potential percent error is
100% x 0.1 g
= 20%
0.5 g
If we assume the quantity 0.0005 g can vary by up to 0.0001 g above or below its nominal value, then the potential percent error is
100% x 0.0001 g
= 20%
0.0005 g
As the above examples show, the relative uncertainty in these two quantities is the same, thus the leading zeros can not be significant. We must always keep in mind that a zero is only significant if its presence imporves the precision of the number. Here, we see the leading zeros do not lower the percent error, so they can not be significant. Notice that a zero's ability to change the value of a number does not make it significant. In this example, 0.5 g does not represent the same mass as 0.0005 g. Thus, the leading zeros change the numerical value of the quantity, but not its precision. It is only the improvement in precision -- and not a change in value -- that can make a zero significant.
Again using percent errors, let us show that the zeros after the decimal point are significant when we compare the quantities 5 g, 5.0 g, and 5.00 g. Here are the relative errors for these quantities:
100% x 1 g
= 20%
5 g
100% x 0.1 g
= 2%
5.0 g
100% x 0.01 g
= 0.2%
5.00 g
In the calculations above, the number in the numerator is the uncertainy and the number in the denominator is the nominal value. Notice that the zeros after the decimal point don't change the nominal value, but they drastically improve the precision of the number. Therefore, these zeros are significant. 5 g has 1 significant figure, 5.0 g has 2 significant figures and 5.00 g has 3 significant figures.
So far, you have seen how to deal with numbers that come from measurements, such as distances measured with a meter stick and masses measured with a balance. But not all numbers come from direct measurements. Another source of numbers is the answers to calculations that use directly measured data. Since the data is not known with absolute certainty, the answers to the calculations can not be known with absolute certainty either. This is true for the fairly obvious reason that if I change the numbers I use in the calculation, I will get a different answer. So we must now look at how the uncertainty in our data will affect our calculations.
Let's suppose I have a rectangular plot of land for which I would like to know the area. Area is not directly measured -- rather, it is calculated. In the case of a rectangle, the calculation is a very simple one. I need to take two measurements -- the length and width of my plot of land. These will be my directly measured data. When I present you with these measurements, you can use significant figure rules you have already learned to determine how many significant figures I am reporting. I will obtain the area by multiplying the length by the width. When you calculate the area based on my measurements, however, you can NOT use the rules you have already learned to obtain the number of significant figures, because the area is not measured -- it is calculated. You will see in the course of this example how we can determine the number of significant figures in the calculated area. After this has arisen naturally, I will then present the formal rule, which hopefully will be more meaningful by then because you have already seen it "work".
Let's say my rectangular plot measures 11.21 m by 4.22 m. Multiplying these numbers on a 10 digit calculator (try it with me -- you will learn better that way) yields the answer 47.3062 m2. If we were to treat this number as "data", we would conclude it has 6 significant figures (applying rules 1 and 4 -- see earlier in these notes, where I present the rules for measured data). This would give an incorrect interpretation, however, because it would suggest that the actual area is somewhere in the range 47.3061 m2 to 47.3063 m2. As well will see in just a minute, the uncertainty in the area is much larger than that.
Let us now look at the measurements from which our area was obtained. The length of the plot of land was 11.21 m, which probably means the actual length is in the range 11.20 m to 11.22 m, with 11.21 m just being our best estimate. Likewise, the width, which was reported as 4.22 m, probably means the actual value is somewhere between 4.21 m and 4.23 m, with 4.22 m being our best estimate. Earlier, I calculated the "nominal" area (that is, using the measured values) to be 47.3062 m2. Now lets also calculate the minimal area (using the low values for both length and width) and the maximal area (using the high values for both length and width). The nominal value is also calculated below, so we will have all 3 values for consideration.
Maximal area = 11.22 m x 4.23 m = 47.4606 m2
Nominal area = 11.21 m x 4.22 m = 47.3063 m2
Minimal area = 11.20 m x 4.21 m = 47.152 m2
In all three calculation results, the first digit is a 4; therefore, the 4 is a "certain" digit. We are sure the number in the first position is a 4. Likewise, in all three calculation results, the second digit is a 7, so we are sure a 7 belongs in the second position, and it is also a "certain"digit. When it comes to the third digit, however, there is uncertainty. The three calculations do not agree on what number should go in the third position, so the number we write in that position is an "uncertain" digit. Recall from earlier in these notes that we are supposed to report one -- but ONLY one -- uncertain digit when we express quantities that have uncertainties. Thus we must express the area as 47.3 m2. In spite of how it appeared when we looked at the number 47.3063, it did not have 6 significant figures, it had only 3.
Fortunately, it will not be necessary to do every calculation 3 times to see how many significant figures the answer will have, because there are some simple rules we can follow that will just let us look at the data and decide how many significant figures the answer will have. We will only have to do the calculation once -- to obtain the nominal answer -- and the rules will tell us how to round off that answer to be properly expressed.
The rule for multiplication and division is that the answer can only have as many significant figures as the number with the fewest significant figures. In the example with the rectangular plot of land, we multiplied 11.21 m (4 significant figures) by 4.22 m (3 significant figures) so that answer can only be expressed to 3 significant figures. Notice that we discovered this without knowing the rule at the time. The rule I just gave you summarizes what you already saw happen. From now on, we will just apply the rule without doing 3 calculations to check it each time.
Addition and subtraction follow a different rule from multiplication and division. Again, I will present an example where we determine the number of significant figures by careful consideration of the uncertainty in the measurements, and after we see what happens, I will present the formal rule.
Let's say I have two pieces of string. One has been measured and found to have a length of 15.2 m and the other to have a length of 1.147 m. What is the combined length of the two pieces of string? In the arithmetic that follows, I will show numbers known for certain in black, numbers that have uncertainty (but which can be reasonably estimated) in red, and numbers that have so much uncertainty we have no idea of their value in purple. Here is how we can represent the addition of the two lengths:
01.147
m
+ 15.200
m
___________
16.347
m
The numbers have been lined up in the usual way, according to their decimal points. I have inserted zeros as needed to give the same number of digits in each number. In the number 01.147, the leading zero is not significant (rule number 2 for data) but we know for sure it is a zero, because if it was something else, the number would be much larger. As you have seen, zeros at the beginning of a number are not significant because they do not improve the precision of the number. This zero is shown in black, because even though it is not a significant digit, it is a "certain" digit. In the number 15.2, I have added two zeros at the end to make this number the same length as the one above it. These zeros are just "place holders" -- we really have no idea what numbers go in these positions -- they could be anything. This is because the 2 is already uncertain, and if we are not even sure of the value at the tenths level, we can't possibly know the hundredths or thousandths. When adding the numbers, however, we treat the number 15.2 as if it had zeros in the second and third decimal places.
When adding the numbers digit by digit in the
usual way, we observe the following common sense rules:
The rule for addition and subtraction is that the answer can only have as many decimal places at the number with the fewest decimal places. In this example, we added the numbers 1.147 m (3 decimal places) and 15.2 m (1 decimal place). Therefore, the answer can only have 1 decimal place. Again, we reached this conclusion without knowing the rule beforehand, and the rule I just gave you summarizes what you already saw happen.
We must now consider what happens when we do long calculations, including those involving mixed arithmetic. In such problems, it is best not to round off the intermediate answers, but you must keep track of the significant figures each step of the way, so you will know how to round the final answer. As an example, let's solve the mixed arithmetic problem
1.216 (1.3 + 3.997)
= ?
2.18995
We need to work this out part by part, following the appropriate significant figure rules in each part. First let's do the addition in the parentheses in the numerator.
1.3 + 3.997 = 5.297
Because this is an intermediate answer rather than a final answer, I have not rounded it off, but have put an underline under the last significant figure (first uncertain digit). If this had been a final answer, I would have rounded it off to 5.3. Our mixed arithmetic problem now looks like this:
1.216 (5.297)
____________ =
?
2.18995
Now let's do the multiplication in the numerator.
1.216 x 5.297 = 6.441152
In the above calculation, the 1.216 is directly measured data, so it has 4 significant figures, but the 5.297 is a calculation result, which has only 2 significant figures. The answer to this problem can therefore only have 2 significant figures. Our mixed arithmetic problem now looks like this:
6.441152
_________ =
?
2.18995
In the final calculation, we do the indicated division. Your 10 digit calculator will give the result as 2.941232448. The number 2.18995 is directly measured data, and has 6 significant figures, but the number 6.441152 is a calculation result and has only 2 significant figures. Therefore, the final answer should be expressed as 2.9.
1.216 (1.3 + 3.997)
= 2.9
2.18995
This particular example will give the same final answer even if you round off the intermediate answers, but that's not always the case. See Example 1.6 on page 18 in your Hill and Petrucci text for an illustration of a case where rounding the intermediate answers makes a difference in the final answer. Remember: its always best NOT to round off the intermediate answers.
The last situation that must be covered here is handling exact numbers. Significant figures are designed to give us an idea of the amount of uncertainty in a quantity, but not all quantities have uncertainty -- some are known exactly (zero uncertainty). Quantities with uncertainties come -- either directly or indirectly -- from measurements. For example, when you measure the length of a plot of land, the result of your measurement has uncertainty, and this value comes directly from a measurement. When you calculate the area based on your measurements of length and width, the area has uncertainty because the uncertainties in your measurements cause uncertainties in your calculated results. This is an example where the uncertainty comes from measurements indirectly. So if no measurements are involved, you may not have uncertainty. When would this happen?
One way to get an exact number is to make a direct count of items that can only come in integer amounts. For example, when I take roll in my chemistry classes, I might report the attendance as 27. Saying there are 27 students in class is very different than saying a piece of string measures 27 m. In the case of the 27 m piece of string, it is possible (in fact, it is even probable) that the string is NOT exactly 27 m, but rather, some other length that is close to 27 m. Even if I measure the string with a finely calibrated ruler and report the length as 27.000 m, it might be 26.999 m or 27.001 m and it just looks like 27.000 m to me. But when I count the number of students in the room and determine that there are 27 students, I don't have to think "maybe there are really 26.999 students and it just looks like 27". Since students only come in whole numbers, when I count 27 students in the room, I can be sure there are exactly 27. So how many significant figures should the number 27 be considered to have in this case? We can make two arguments to show that such a number should have an infinite number of significant figures.
The first way to arrive at this conclusion is to note that significant figures are supposed to tell us how much uncertainty there is in the number. The more significant figures we have, the better we know the number and the less uncertainty. But an EXACT number has NO UNCERTAINTY, so it is not possible to improve on it. If we assigned any finite number of significant figures to the number, its precision could be improved upon by obtaining a greater number of signifciant figures. The only way not to be able to improve the precision of the number is for it to have an infinite number of significant figures, becasue you can't get larger than infinity.
Another way to arrive at this conclusion is to note that the digits after the decimal point are known for certain. I am SURE there are no tenths of a student, no hundredths of a student, and so on since people don't come in fractions. The number of students in the room is 27.00000..... where I could go on writing zeros forever. Are these zeros significant? Recall that zeros after a decimal point are significant if they are preceeded anywhere in the number by non-zero digits (Rules for Data, rule 3). This makes the zeros significant, and I could write an infinite number of such zeros, therefore the number has an infinite number of significant figures. Of course, numbers like this, which are inherently integers, we normally write just write as integers (27 in this case) but we understand the number of significant figures is infinite. There is no point writing any trailing zeros, because we can never write all that belong there, since there is an infinite number of them.
Another way exact numbers arise is when we define a unit of measurement. For example, when we say 1 foot is a distance of 12 inches, we should not interpret the number 12 as having 2 significant figures. This would be saying the value is assumed to be somewhere between 11 inches and 13 inches, with 12 inches being the best estimate. However, in this case, a foot is defined to be exactly 12 inches. Thus, the number of significant figures is infinite. We could say a foot is 12.0000000..... inches, where we could go on writing the zeros forever. As explained previously, all of these zeros (an infinite number) are significant.
When exact numbers arise in your work in this course, it will usually be during conversions of one unit to another. For example, consider the problem "Express a length of 3.116 ft in units of inches". The calculation looks like this:
3.116 ft x
12 in = 37.392 in
= 37.39 in
1 ft
A common error in expressing the result of the above calculation is to round off the answer as 37 in. This error results from taking the number 12 to have only 2 significant figures. Since the number 2 is less than the number 4 (3.116 ft has 4 significant figures) the final answer is incorrectly rounded off to 2 significant figures. However, when we realize that the 12 has an infinite number of significant figures in this calculation, it is the 3.116, and not the 12, that has the fewest significant figures. Realizing this, we round off the answer to 4 significant figures and express it as 37.39 in.
FURTHER READING
Read pages 15 - 18 of your Hill and Petrucci text. This includes the sections "Significant Figures", which presents the rules for directly measured data, "Significant Figures in Calculations: Multiplication and Division", and "Significant Figures in Calculations: Addition and Subtraction". These pages cover the same material I have covered in these notes, so they should reinforce what you have learned here.
Note: If you don't have the book, please be advised
that I have placed a copy on two-hour reserve (in-library use only) at
the Learning Resources Center. You can go to the circulation desk
and ask for the book "General Chemistry, An Integrated Approach", Second
Edition by Hill and Petrucci. I have also provided (two-hour reserve,
in-library use only) the study guide, and solutions manual that go with
this book. Happy Reading!
This page was last modified Tuesday June 6, 2000