Counting Atoms in Chemical Formulas
When expressing chemical information on paper, we will make frequent
use of the chemical symbols in the periodic table. For now, let us
take the chemical symbol of an element to stand for one atom of that
element. Later, we will develop a different interpretation, but for
now, the present one will suffice.
Examples:
H represents one atom of hydrogen
C represents one atom of carbon
Mg represents one atom of magnesium
We write chemical formulas for compounds. A compound will be either
ionic or molecular. If molecular, the atoms are held together by
sharing electrons. Atoms held together by sharing electrons are
said to be covalently bonded. A group of covalently bonded atoms is
called a molecule.
For molecular compounds, we can write a molecular formula which
indicates the number of atoms of each element in the molecule.
For example, two atoms of hydrogen and one atom of oxygen combine
(share electrons) to form a molecule of water. As everyone knows,
we represent water as H2O. This formula tells us that
2 atoms of hydrogen and one atom of oxygen are present in the molecule.
Sometimes it is necessary to have more than one atom of an element, or
more than one molecule of a compound. In these cases, we can write
a number in front of the element symbol or chemical formula to indicate
the number of atoms or molecules involved.
2Al represents 2 atoms of aluminum
4 Mg represents 4 atoms of magnesium
5H2O represents 5 molecules of water
3C12H22O11 represents 3 molecules of
sucrose (table sugar).
The numbers that appear in front of the symbols and formulas above are
called coefficients. The coefficients tell us the number
of atoms (for chemical symbols) or molecules (for molecular formulas)
that we are dealing with. The small numbers that appear somewhat
below the chemical symbols within chemical formulas are called
subscripts. The subscripts tell us how many atoms of
each element are in the molecule. For both coefficients and
subscripts, we generally don't write their value when it is equal to 1,
because a 1 is "understood" if no coefficient or subscript is written.
Many elements (for example, aluminum and magnesium, as shown above) are
monatomic, that is, they consist of individual atoms. An
aluminum can, for example, is a collection of a very large number of
aluminum atoms (ignoring the label that has been painted on the can).
There are a few elements, however, that exist as molecules. There are
7 elements that exist as diatomic molecules. That is, the fundamental
particles that make up a sample of these elements are pairs of atoms,
rather than individual atoms.
Oxygen exists as O2.
Nitrogen exists as N2.
Hydrogen exists as H2.
Fluorine exists as F2.
Chlorine exists as Cl2.
Bromine exists as Br2.
Iodine exists as I2.
There are also a few elements that exist as molecules that have more than
2 atoms:
The form of oxygen called ozone exists as O3.
The form of phosphorous called white phosphorous exists as P4.
Sulfur is normally encountered as S8.
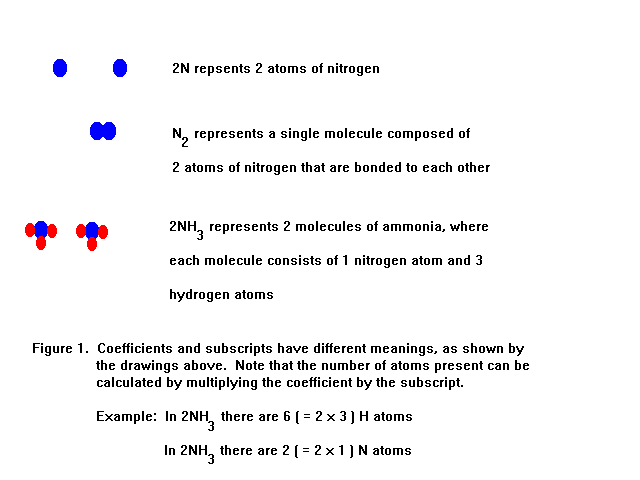
Note that 2N and N2 do not mean the same thing. 2N
represents 2 individual atoms of nitrogen that are NOT bonded to
each other. But N2 represents a single entity that we call a
molecule. It consists of 2 nitrogen atoms that ARE bonded to each
other.
You can count the number of atoms of each element in a chemical formula by
multiplying the coefficient by the subscript, recognizing that those
coefficients and subscripts that are not shown are equal to 1. For
example, if we write 2NH3 (which is 2N1H3)
we calculate the number of atoms as follows:
For N we have 2 x 1 = 2
For H we have 2 x 3 = 6
Thus, in 2 molecules of NH3, you have a total of 2 N atoms and 6
H atoms. This is shown in Figure 1.
The compounds considered so far have all been molecular compounds.
Ionic compounds do not exist as molecules. Rather than having atoms
being joined together by sharing electrons, one or more atoms lose
electrons (thereby becoming positive ions) and these electrons are then
gained by one or more other atoms (thereby becoming negative ions).
Since opposite charges attract one another, the positive and negative ions
are held together to form (at room temperature, and even well above) a
solid crystal.
Ionic compounds always form in such a way that the total positive
charge is equal to the total negative charge. In this way, the ionic
crystal as a whole is electrically neutral. Because there are no
discrete molecules in such compounds, all we can do in expressing the
chemical formula of these substances is to express the ratio of positive
ions to negative ions. Consider ordinary table salt as an example.
Chemically, we know it as sodium chloride, NaCl. Sodium forms the ion
Na+ and chlorine forms the ion Cl- (which we call the
chloride ion). Since these ions have equal and opposite charges,
there must be an equal number of Na+ ions and Cl-
ions. The simplest way to express this is a one-to-one ratio.
Thus, the formula of sodium chloride is written NaCl. On paper,
ionic formulas often don't look any different than molecular formulas, but we
must be aware that it is not correct to say that NaCl represents a molecule
of sodium chloride. Rather, we say that NaCl represents a formula unit
of sodium chloride. It is true that for every Na+ ion in
the crystal, there is a Cl- ion. However, we can not
identify any particular Cl- ion as "belonging" to any
particular Na+ ion. In the case of a molecule,
particular atoms can be identified as belonging to each other -- that is,
being part of the same group of atoms that make up a particular molecule.
We take the formula unit of an ionic compound to represent the smallest
possible amount of that compound, in the same way that we take a
molecule to represent the smallest possible amount of a molecular
compound. Thus the smallest quantity of sodium chloride that we can
have -- and still recognize it as sodium chloride -- is one sodium ion and
one chloride ion.
Often, it is no more difficult to count the atoms in ionic formulas than
it is in molecular formulas. Consider the following examples:
MgCl2:
For Mg we have 1 x 1 = 1 (1 Mg2+ ion in formula)
For Cl we have 1 x 2 = 2 (2 Cl- ions in formula)
2Al2O3:
For Al we have 2 x 2 = 4 (4 Al3+ ions total in the two formula units)
For O we have 2 x 3 = 6 (6 O2- ions total in the two formula units)
It becomes slightly more difficult to count the atoms in ionic formulas when
they contain polyatomic ions that occur more than once in the formula.
In these cases, the subscrips within the polyatomic ion must be multiplied
by the subscript that appears outside the parentheses. If a
coefficient is present, it must also be multiplied, meaning sometimes
there will be three numbers to multiply together to calculate the number
of atoms of a particular element. Consider the following examples:
(NH4)2CO3:
For N we have 1 x 2 = 2 (multiplying subscript of N by subscript of group)
For H we have 4 x 2 = 8 (multiplying subscript of H by subscript of group)
For C we have 1 (coefficient of formula, subscript of C and subscript of group are all 1)
For O we have 3 (subscript of O is 3, coefficient of formula and subscript of group are 1)
If you have trouble understanding the above, it may help to recall that
(NH4)2CO3 is literally
1(NH4)2(CO3)1.
Written in this form, you can clearly see the coefficient in front of the
formula, and the subscript of the carbonate group, both of which are 1.
A still more complicated case is when an element appears in more than one
place in the formula. For example, lets count the atoms in
5(NH4)2HPO4. We must be careful
because H atoms appear both in the NH4 group and in the
HPO4 group. The entire formula is taken 5 times, and
each formula includes the NH4 group twice. Overall, we
have 10 NH4 groups and 5 HPO4 groups.
For N we have 5 * 1 * 2 = 10
(multiplying coefficeint,
subscript within group, and subscript outside of group)
For H we have 5 * 4 * 2 + 5 * 1 * 1 = 40 + 5 = 45
(for each group, multiplying coefficient, subscript in group and subscript
outside of group)
For P we have 5 * 1 * 1 = 5
(Multiplying coefficeint, subscript within group, and subscript outside
group)
For O we have 5 * 4 * 1 = 20
(Multiplying coefficient, subscript within group, and subscript outside
group)
If you have trouble understanding the above, it may help to recall that
5(NH4)2HPO4 is literally
5(NH4)2(HPO4)1. Written
in this way, the subscript of the HPO4 group is clearly
visible. However, while writing it this way may help with problem
solving, we must keep in mind that 1's are not usually written as
coefficients or subscripts.
This page was last modified Friday October 8, 1999
